
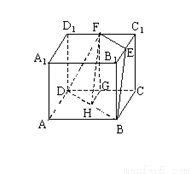
(14分)如图2-72,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是B1C1、C1D1的中点,
(1)求证:E、F、B、D四点共面;
(2)求四边形EFDB的面积.
(1)见解析;(2)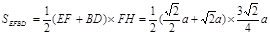 =
=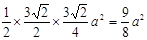
【解析】
试题分析:⑴证明:如答图所示,连结B1D1,在△C1B1D1中,C1E=EB1,C1F=FD1 ,∴EF//B1D1,且EF=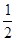 B1D1,又A1A
B1D1,又A1A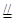 B1B,A1A
B1B,A1A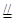 D1D,∴B1B
D1D,∴B1B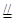 D1D,∴四边形BB1D1D是平行四边形. ∴B1D//BD,EF//BD,∴E、F、D、B四点共面
D1D,∴四边形BB1D1D是平行四边形. ∴B1D//BD,EF//BD,∴E、F、D、B四点共面
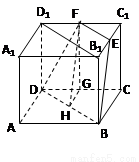
⑵由AB=a,知BD=B1D1=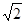 a,EF=
a,EF=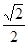 a,
a,
DF=BE=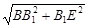 =
=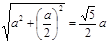 ,
,
过F作FH⊥DB于H,则DH=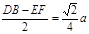
∴FH=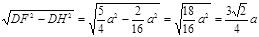
四边形的面积为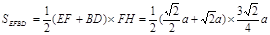 =
=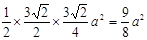
考点:本题主要考查正方体的特征、平面的基本性质以及平面图形的面积计算,考查空间想象能力及逻辑推理论证能力。
点评:空间问题注意转化成平面问题,这是解答立体几何问题的基本思路。


 一课一练课时达标系列答案
一课一练课时达标系列答案科目:高中数学 来源:2012年苏教版高中数学必修2 1.2点、线、面之间的位置关系练习卷(解析版) 题型:解答题
(14分)如图2-72,棱长为a的正方体ABCD-A1B1C1D1中,E、F分别是B1C1、C1D1的中点
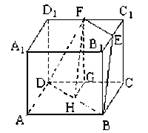
(1)求证:E、F、B、D四点共面;
(2)求四边形EFDB的面积.
查看答案和解析>>
科目:高中数学 来源: 题型:
|
(1)求证:E、F、B、D四点共面;
(2)求四边形EFDB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com