
已知一颗粒子等可能地落入如右图所示的四边形 内的任意位置,如果通过大量的实验发现粒子落入△
内的任意位置,如果通过大量的实验发现粒子落入△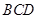 内的频率稳定在
内的频率稳定在 附近,那么点
附近,那么点 和点
和点 到时直线
到时直线 的距离之比约为( )
的距离之比约为( )
A. | B. | C. | D. |
D
解析试题分析:设粒子落入△BCD内的频率为P1粒子落入△BAD内的频率为P2
点A和点C到时直线BD的距离d1,d2,根据题意:P2=1-P1=1- =
=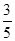 ,然后根据
,然后根据
P1=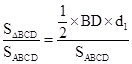 ,P2=
,P2=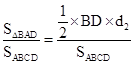 ,P2:P1= d2: d1=3:2,故选D.
,P2:P1= d2: d1=3:2,故选D.
考点:本试题主要考查了几何概型中的面积类型及其应用,基本方法是:分别求得构成事件A的区域面积和试验的全部结果所构成的区域面积,两者求比值,即为概率
点评:解决该试题的关键是先明确是几何概型中的面积类型,称设粒子落入△BCD内的频率为P1粒子落入△BAD内的频率为P2,点A和点C到时直线BD的距离d1,d2求得P2,利用其面积之比即为概率之比,再由三角形共底,求得高之比.


 红果子三级测试卷系列答案
红果子三级测试卷系列答案 课堂练加测系列答案
课堂练加测系列答案科目:高中数学 来源: 题型:单选题
投掷一枚质地均匀的骰子两次,若第一次面向上的点数小于第二次面向上的点数我们称其为前效实验,若第二次面向上的点数小于第一次面向上的点数我们称其为后效实验,若两次面向上的点数相等我们称其为等效试验.那么一个人投掷该骰子两次后出现等效实验的概率是( )
A. | B.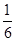 | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
一个坛子里有编号为1,2,…,12的12个大小相同的球,其中1到6号球是红球,其余的是黑球,若从中任取两个球,在取到的都是红球的前提下,且至少有1个球的号码是偶数的概率是( )
A. | B.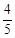 | C. | D. |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
先后抛掷两颗骰子,设出现的点数之和是10,11,12的概率依次是P1,P2,P3,则( )
| A.P1>P2>P3 | B.P1>P2=P3 | C.P1=P2>P3 | D.P1=P2<P3 |
查看答案和解析>>
科目:高中数学 来源: 题型:单选题
甲乙两艘轮船都要在某个泊位停靠6小时,假定他们在一昼夜的时间段中随机地到达,试求这两艘船中至少有一艘在停泊位时必须等待的概率( )
A.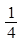 | B. | C. | D. |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com