
| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
分析 换元可得y=f(x)=$\frac{{x}^{2}+x-5}{x-2}$=t+$\frac{1}{t}$+5,从而利用基本不等式求函数的最小值.
解答 解:令x-2=t,t>0;
y=f(x)=$\frac{{x}^{2}+x-5}{x-2}$
=$\frac{(t+2)^{2}+t+2-5}{t}$
=$\frac{{t}^{2}+5t+1}{t}$
=t+$\frac{1}{t}$+5≥7
(当且仅当t=1,即x=3时,等号成立),
故函数f(x)=$\frac{{x}^{2}+x-5}{x-2}$,x∈(2,+∞)的最小值为7,
故选D.
点评 本题考查了换元法的应用及基本不等式在求最值时的应用.


 学习实践园地系列答案
学习实践园地系列答案科目:高中数学 来源: 题型:选择题
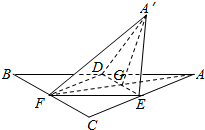 如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )
如图,正△ABC的中线AF与中位线DE相交于G,已知△A′ED是△AED绕DE旋转过程中的一个图形,下列命题中,错误的是( )| A. | 动点A′在平面ABC上的射影在线段AF上 | |
| B. | 恒有DE⊥平面A′GF | |
| C. | 三棱锥A′-FED的体积有最大值 | |
| D. | 异面直线A′E与BD不可能垂直 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
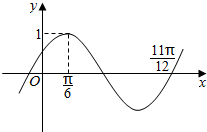 函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图示,将y=f(x)的图象向右平移$\frac{π}{6}$个单位后得到函数y=g(x)的图象,则g(x)的单凋递增区间为( )
函数f(x)=Asin(ωx+φ)(A>0,ω>0,|φ|<$\frac{π}{2}$)的部分图象如图示,将y=f(x)的图象向右平移$\frac{π}{6}$个单位后得到函数y=g(x)的图象,则g(x)的单凋递增区间为( )| A. | [2kπ-$\frac{π}{6}$,2kπ$+\frac{π}{3}$] | B. | [2k$π+\frac{π}{3}$,2kπ$+\frac{5π}{6}$] | C. | [kπ$+\frac{π}{3}$,kπ$+\frac{5π}{6}$] | D. | [kπ$-\frac{π}{6}$,kπ$+\frac{π}{3}$], |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (2,4] | B. | [-2,4] | C. | [4,+∞) | D. | (-∞,-2]∪[4,+∞) |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com