
分析 求出函数f(x)=x2+2x+alnx在区间(0,1)内无极值点的a的范围,从而求出函数有极值的范围即可.
解答 解:函数f(x)=x2+2x+alnx在区间(0,1)内无极值
?函数f(x)=x2+2x+alnx在区间(0,1)内单调,
?函数f′(x)≥0或f′(x)≤0a∈R)在(0,1)内恒成立,
由f′(x)=2x+2+$\frac{a}{x}$≥0在(0,1)内恒成立,
?a≥(-2x-2x2)max,x∈(0,1),即a≥0,
由f′(x)=2x+2+$\frac{a}{x}$≤0在(0,1)内恒成立,
?a≤(-2x-2x2)min,x∈(0,1),即a≤-4,
故f(x)在区间(0,1)上有极值,
则-4<a<0,
故答案为:(-4,0).
点评 本题考查了利用导数研究函数的单调性极值与最值、分离参数法、函数的单调性等基础知识与基本技能方法,考查了推理能力和计算能力.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 384 | B. | 768 | C. | -$\frac{3}{512}$ | D. | -$\frac{3}{1024}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | ($\frac{8}{3}$,$\frac{28}{5}$) | B. | ($\frac{8}{3}$,$\frac{28}{5}$] | C. | ($\frac{8}{3}$,$\frac{18}{5}$) | D. | ($\frac{8}{3}$,$\frac{18}{5}$] |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
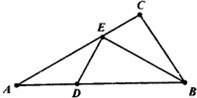 如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,交AC于点E,过点E作ED⊥BE交AB于点D.
如图,在Rt△ABC中,∠C=90°,BE平分∠ABC,交AC于点E,过点E作ED⊥BE交AB于点D.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com