
(12分)如图,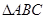 的角平分线AD的延长线交它的外接圆于点E
的角平分线AD的延长线交它的外接圆于点E
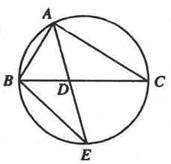
(I)证明: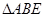
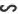
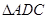
(II)若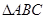 的面积
的面积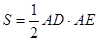 ,求
,求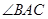 的大小。
的大小。
(1)见解析;(2) =90°.
=90°.
【解析】相似三角形有三个判定定理:判定定理1:两角对应相等的两个三角形相似; 判定定理2:三边对应成比例的两个三角形相似;判定定理3:两边对应成比例,并且夹角相等的两个三角形相似.在证明三角形相似时,要根据已知条件选择适当的定理.
(1)要判断两个三角形相似,可以根据三角形相似判定定理进行证明,但注意观察已知条件中给出的是角的关系,故采用判定定理1更合适,故需要再找到一组对应角相等,由圆周角定理,易得满足条件的角.
(2)根据(1)的结论,我们可得三角形对应对成比例,由此我们可以将△ABC的面积S=12
AD•AE转化为S=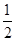 AB•AC,再结合三角形面积公式,不难得到∠BAC的大小.
AB•AC,再结合三角形面积公式,不难得到∠BAC的大小.
证明:
(Ⅰ)由已知条件,可得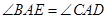
因为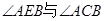 是同弧上的圆周角,所以
是同弧上的圆周角,所以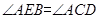
故△ABE∽△ADC. ……5分
(Ⅱ)因为△ABE∽△ADC,所以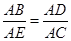 ,即AB·AC=AD·AE.
,即AB·AC=AD·AE.
又S=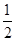 AB·ACsin
AB·ACsin ,且S=
,且S=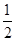 AD·AE,故AB·ACsin
AD·AE,故AB·ACsin =
AD·AE.
=
AD·AE.
则sin =1,又
=1,又 为三角形内角,所以
为三角形内角,所以 =90°.
……10分
=90°.
……10分


科目:高中数学 来源:2011年湖南省普通高等学校招生统一考试文科数学 题型:解答题
(本题满分12分)
如图3,在圆锥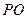 中,已知
中,已知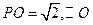 的直径
的直径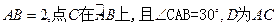 的中点.
的中点.
(I)证明:
(II)求直线和平面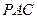 所成角的正弦值.
所成角的正弦值.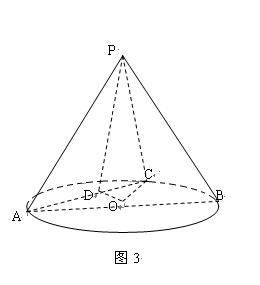
查看答案和解析>>
科目:高中数学 来源:2015届河南灵宝三中高一上第三质检数学试卷(解析版) 题型:解答题
(本小题满分12分)如图是从上下底面处在水平状态下的棱长为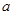 的正方体
的正方体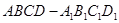 中分离出来的:
中分离出来的:
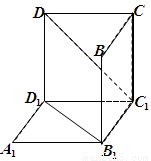
(1)试判断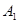 是否在平面
是否在平面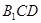 内;(回答是与否)
内;(回答是与否)
(2)求异面直线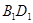 与
与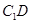 所成的角;
所成的角;
(3)如果用图示中这样一个装置来盛水,那么最多可以盛多少体积
查看答案和解析>>
科目:高中数学 来源:2013届山东省高三第二次质量检测理科数学试卷(解析版) 题型:解答题
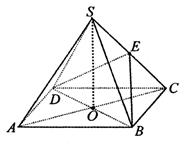
(本题满分12分)如图,四棱锥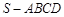 中,底面
中,底面 是边长为4的正方形,
是边长为4的正方形,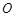 是
是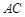 与
与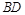 的交点,
的交点,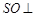 平面
平面 ,
,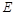 是侧棱
是侧棱 的中点,异面直线
的中点,异面直线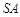 和
和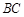 所成角的大小是60
所成角的大小是60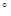 .
.
(Ⅰ)求证:直线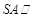 平面
平面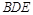 ;
;
(Ⅱ)求直线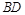 与平面
与平面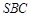 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源:河北省2010年高三一模模拟(三)数学文 题型:解答题
(本题满分12分)
如图,在直三棱柱ABC-A1B1C1中,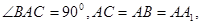 E是BC的中点。
E是BC的中点。
(1)求异面直线AE与A1C所成的角;
(2)若G为C1C上一点,且EG⊥A1C,试确定点G的位置;
|
查看答案和解析>>
科目:高中数学 来源:2010-2011年广西省高二下学期期中考试数学 题型:解答题
((本小题满分12分)
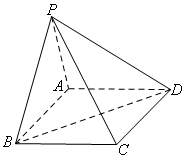
如图,在四棱锥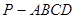 中,底面
中,底面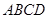 是矩形.已知
是矩形.已知
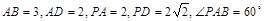 .
.
(1)证明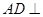 平面
平面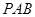 ;
;
(2)求异面直线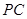 与
与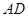 所成的角的大小;
所成的角的大小;
(3)求二面角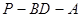 的大小.
的大小.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com