已知a>0,f(x)=ax2-2x+1+ln(x+1),l是曲线y=f(x)在点P(0,f(0))处的切线.
(1)求切线l的方程;
(2)若切线l与曲线y=f(x)有且只有一个公共点,求a的值.
【答案】
分析:(1)根据导数的几何意义求出函数f(x)在x=0处的导数,从而求出切线的斜率,再用点斜式写出切线方程,化成斜截式即可.
(2)将切线l与曲线y=f(x)有且只有一个公共点等价于方程ax
2-2x+1+ln(x+1)=-x+1即ax
2-x+ln(x+1)=0有且只有一个实数解.
令h(x)=ax
2-x+ln(x+1),求出h'(x),然后讨论a与

的大小,研究函数的单调性,求出满足使方程h(x)=0有一解x=0的a的取值范围即可.
解答:解:(1)∵f(x)=ax
2-2x+1+ln(x+1)∴f(0)=1
∴f'(x)=

∴f′(0)=-1
切点p(0,1),切线l的斜率为-1∴切线l的方程:y=-x+1;
(2)切线l与曲线y=f(x)有且只有一个公共点等价于方程
ax
2-2x+1+ln(x+1)=-x+1即ax
2-x+ln(x+1)=0有且只有一个实数解.
令h(x)=ax
2-x+ln(x+1),∵h(0)=0
∴方程h(x)=0有一解x=0
h'(x)=2ax-1+
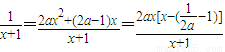
①若a=

,则h'(x)=
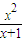
≥0(x>-1),
∴h(x)在(-1,+∞)上单调递增,
∴x=0是方程h(x)=0的唯一解;
②若0<a<

,则h′(x)=0两根x
1=0,x
2=
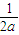
-1>0

∴
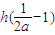
<h(0)=0,而
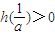
∴方程h(x)=0在
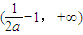
上还有一解,则h(x)=0解不唯一;
③若a>

,则h′(x)=0两根x
1=0,x
2=
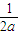
-1∈(-1,0)
同理可得方程h(x)=0在
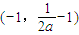
上还有一解,
则h(x)=0解不唯一
综上,当切线l与曲线y=f(x)有且只有一个公共点时,a=

.
点评:本题主要考查了利用导数研究曲线上某点切线方程,以及利用导数研究函数的单调性,同时考查了转化与划归的思想,以及计算能力,属于中档题,综合题.

 的大小,研究函数的单调性,求出满足使方程h(x)=0有一解x=0的a的取值范围即可.
的大小,研究函数的单调性,求出满足使方程h(x)=0有一解x=0的a的取值范围即可. ∴f′(0)=-1
∴f′(0)=-1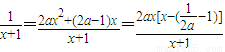
 ,则h'(x)=
,则h'(x)=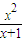 ≥0(x>-1),
≥0(x>-1), ,则h′(x)=0两根x1=0,x2=
,则h′(x)=0两根x1=0,x2=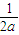 -1>0
-1>0
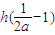 <h(0)=0,而
<h(0)=0,而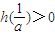
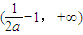
 ,则h′(x)=0两根x1=0,x2=
,则h′(x)=0两根x1=0,x2=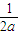 -1∈(-1,0)
-1∈(-1,0)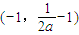 上还有一解,
上还有一解, .
.
