
若向量![]() 与
与![]() 不共线,且|
不共线,且|![]() |=4,|
|=4,|![]() |=3.
|=3.
(Ⅰ)k为何值时,向量![]() +k
+k![]() 与
与![]() ﹣k
﹣k![]() 互相垂直;
互相垂直;
(Ⅱ)若(2![]() ﹣3
﹣3![]() )(2
)(2![]() +
+![]() )=61,求
)=61,求![]() 与
与![]() 的夹角θ.
的夹角θ.
考点:
平面向量数量积的运算;数量积表示两个向量的夹角.
专题:
平面向量及应用.
分析:
(Ⅰ)![]() +k
+k![]() 与
与![]() ﹣k
﹣k![]() 垂直时,(
垂直时,(![]() +k
+k![]() )•(
)•(![]() ﹣k
﹣k![]() )=0,利用数量积运算即可解得k值;(Ⅱ)利用数量积的运算性质及数量积及数量积定义化简等式可求得答案;
)=0,利用数量积运算即可解得k值;(Ⅱ)利用数量积的运算性质及数量积及数量积定义化简等式可求得答案;
解答:
解:(Ⅰ)![]() +k
+k![]() 与
与![]() ﹣k
﹣k![]() 垂直时,(
垂直时,(![]() +k
+k![]() )•(
)•(![]() ﹣k
﹣k![]() )=0,
)=0,
所以![]() ,即16﹣9k2=0,解得k=
,即16﹣9k2=0,解得k=![]() ,
,
所以当k=![]() 时,向量
时,向量![]() +k
+k![]() 与
与![]() ﹣k
﹣k![]() 互相垂直;
互相垂直;
(Ⅱ)(2![]() ﹣3
﹣3![]() )•(2
)•(2![]() +
+![]() )=61,即
)=61,即![]() ,
,
所以4×42﹣4×4×3cosθ﹣3×32=61,解得cosθ=![]() ,
,
所以![]() 与
与![]() 的夹角θ为120°.
的夹角θ为120°.
点评:
本题考查平面向量数量积的运算、数量积表示两个向量的夹角,属中档题.


 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案 新活力总动员暑系列答案
新活力总动员暑系列答案科目:高中数学 来源:2012年苏教版高中数学必修4 2.5向量的应用练习卷(解析版) 题型:选择题
若向量 与
与 不共线,
不共线,  ·
· ≠0,且
≠0,且 =
= -(
-( )
)  ,则向量
,则向量 与
与 的夹角为( )
的夹角为( )
A.0
B.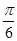 C.
C.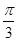 D.
D.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年山东省泰安市高一(下)期末数学试卷(解析版) 题型:解答题
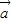 与
与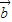 不共线,且|
不共线,且|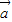 |=4,|
|=4,|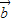 |=3.
|=3.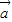 +k
+k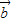 与
与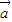 -k
-k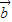 互相垂直;
互相垂直;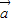 -3
-3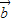 )(2
)(2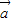 +
+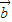 )=61,求
)=61,求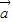 与
与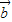 的夹角θ.
的夹角θ.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com