
设随机变量![]() 与η的分布列为:
与η的分布列为:
P(![]() =k)=
=k)=![]() pk(1-p)2-k,k=0,1,2;
pk(1-p)2-k,k=0,1,2;
P(η=m)=![]() pm(1-p)4-m,m=0,1,2,3,4.
pm(1-p)4-m,m=0,1,2,3,4.
已知P(![]() ≥1)=
≥1)=![]() ,求P(η≥1).
,求P(η≥1).
科目:高中数学 来源: 题型:
(本小题共12分)
本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的收费标准为2元(不足1小时的部分按1小时计算)。有人独立来该租车点则车骑游。各租一车一次。设甲、乙不超过两小时还车的概率分别为![]() ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为![]() ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。
(Ⅰ)求甲、乙两人所付租车费用相同的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和为随机变量![]() ,求
,求![]() 的分布列与数学期望
的分布列与数学期望![]() ;
;
查看答案和解析>>
科目:高中数学 来源:2010年北京市崇文区高三年级二模理科试题 题型:解答题
( 本小题共13分)
本小题共13分)
某学校高一年级开设了 五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修
五门选修课.为了培养学生的兴趣爱好,要求每个学生必须参加且只能选修 一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
一门课程.假设某班甲、乙、丙三名学生对这五门课程的选择是等可能的.
(Ⅰ)求甲、乙、丙三名学生参加五门选修课的所有选法种数;
(Ⅱ)求甲、乙、丙三名学生中至少有两名学生选修同一门课程的概率;
(Ⅲ)设随机变量 为甲、乙、丙这三名学生参加
为甲、乙、丙这三名学生参加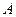 课程的人数,求
课程的人数,求 的分布列与数学期望.
的分布列与数学期望.
查看答案和解析>>
科目:高中数学 来源:2012-2013学年湖南省元月考理科数学试卷(解析版) 题型:解答题
(本小题满分12分)本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租不超过两小时免费,超过两小时的部分每小时收2元(不足1小时的部分按1小时计算)。有人独立来该租车点租车骑游。各租一车一次。设甲、乙不超过两小时还车的概率分别为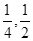 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为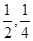 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。
(Ⅰ)求甲、乙两人所付租车费用相同的概率;
(Ⅱ)求甲、乙两人所付的租车费用之和为随机变量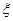 ,求
,求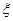 的分布列与数学期望
的分布列与数学期望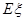 .
.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河南省高三下学期综合考试验收5理科数学 题型:解答题
(本小题满分12分)
本着健康、低碳的生活理念,租自行车骑游的人越来越多。某自行车租车点的收费标准是每车每次租车时间不超过两小时免费,超过两小时的部分每小时收费标准为2元(不足1小时的部分按1小时计算)。有甲乙两人相互独立来该租车点租车骑游(各租一车一次),设甲、乙不超过两小时还车的概率分别为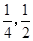 ;两小时以上且不超过三小时还车的概率分别为
;两小时以上且不超过三小时还车的概率分别为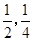 ;两人租车时间都不会超过四小时。
;两人租车时间都不会超过四小时。
(Ⅰ)求出甲、乙两人所付租车费用相同的概率;
(Ⅱ)设甲、乙两人所付的租车费用之和为随机变量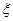 ,求
,求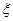 的分布列与数学期望
的分布列与数学期望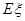 ;
;
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省深圳市高三第一次调研理科数学 题型:解答题
(本小题满分13分)
随机调查某社区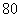 个人,以研究这一社区居民在
个人,以研究这一社区居民在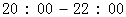 时间段的休闲方
时间段的休闲方
式与性别的关系,得到下面的数据表:
|
休闲方式 性别 |
看电视 |
看书 |
合计 |
|
男 |
|
|
|
|
女 |
|
|
|
|
合计 |
|
|
|
(1)将此样本的频率估计为总体的概率,随机调查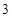 名在该社区的男性,设调查的
名在该社区的男性,设调查的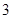 人
人
在这一时间段以看书为休闲方式的人数为随机变量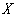 ,求
,求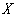 的分布列和期望;
的分布列和期望;
(2)根据以上数据,能否有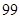 %的把握认为“在
%的把握认为“在 时间段的休闲方式与
时间段的休闲方式与
性别有关系”?
参考公式: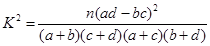 ,其中
,其中 .
.
参考数据:
|
|
|
|
|
|
|
|
|
|
|
|
|
|
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com