Question

方程ax²+ay²-4（a-1）x+4y=0表示圆，求a的取值范围，并求出其中半径最小的圆的方程．

Answer 1

【答案】分析：（1）由圆的标准方程（x-a）²+（y-b）²=r²中r＞0，则r²＞0，求出a的取值范围；
（2）利用配方法求r²的最小值，进一步求出半径最小的圆的方程．
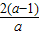
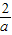
解答：解：（1）∵a≠0时，方程为[x-]²+（y+）²=，
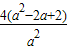
由于a²-2a+2=（a-1）²+1＞0恒成立，
∴a≠0且a∈R时方程表示圆．
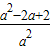
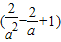
（2）∵r²=4•=4=4[2（-）²+]，
∴a=2时，r_min²=2．
此时圆的方程为（x-1）²+（y+1）²=2．
点评：本题主要考查圆的标准方程，同时考查配方法．