试题分析:解:设f(x)=|x-4|+|x-3|,当x<3时,f(x)=-(x-4)-(x-3)=-2x+7,
故此时有f(x)=-2x+7>1.,当x>4,f(x)=(x-4)+(x-3)=2x-7,,故此时有f(x)=2x-7>1.,当3≤x≤4,f(x)=-(x-4)+(x-3)=1,,综上所述f(x)的最小值为1,,又因为原不等式|x-4|+|x-3|<a有实数解,只要a大于f(x)的最小值即可.,所以a的取值范围是(1,+∞).故选B.
点评:此题主要考查绝对值不等式的解法,对于含有一个绝对值的不等式可以直接去绝对值号求解,对于含有两个绝对值号的绝对值不等式需要用分类讨论的方法去绝对值号.同学们需要注意选择合适的解法

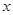 满足不等式
满足不等式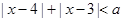 ,则实数
,则实数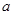 的取值范围是( )
的取值范围是( )




