
(09年临沂高新区实验中学质检)(12分)
函数y=f(x)是定义域为R的奇函数,且对任意的x∈R,均有f(x+4)=f(x)成立,当x∈(0,2)时,f(x)=-x2+2x+1.
(1)当x∈[4k-2,4k+2](k∈Z)时,求函数f(x)的表达式;
(2)求不等式f(x)>![]() 的解集.
的解集.
解析:(1)当x=0时,∵f(0)=-f(0),∴f(0)=0. 1分
当x∈[-2,0]时,-x∈(0,2),
f(x)=-f(-x)=-(x2-2x+1)=x2+2x-1. 3分
由f(x+4)=f(x),知f(x)为周期函数,且周期T=4. 4分
当x∈[4k-2,4k](k∈Z)时,x-4k∈[-2,0],
∴f(x)=f(x-4k)=(x-4k)2+2(x-4k)-1. 5分
当x∈(4k,4k+2)(k∈Z)时,x-4k∈(0,2),
∴f(x)∈f(x-4k)=-(x-4k)2+2(x-4k)+1. 6分
故当x∈[4k-2,4k+2](k∈Z)时,f(x)的表达式为
f(x)= 7分
7分
(2)当x∈[-2,2]时,由f(x)>![]() 得
得 或
或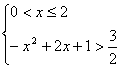
解得1-![]() 10分
10分
∵f(x)是以4为周期的周期函数,
∴f(x)>![]() 的解集为|x|4k+1-
的解集为|x|4k+1-![]() |. 12分
|. 12分


科目:高中数学 来源: 题型:
(09年临沂高新区实验中学质检)已知函数![]() ,当
,当![]() 时,
时,![]() 只有一个实数根;当
只有一个实数根;当![]() 3个相异实根,现给出下列4个命题:
3个相异实根,现给出下列4个命题:
①函数![]() 有2个极值点; ②函数
有2个极值点; ②函数![]() 有3个极值点;
有3个极值点;
③![]() =4,
=4,![]() =0有一个相同的实根 ④
=0有一个相同的实根 ④![]() =0和
=0和![]() =0有一个相同的实根
=0有一个相同的实根
其中正确命题的个数是 ( )
A.1 B.2 C.3 D.4
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com