
一条抛物线的准线方程为y=![]() ,焦点在射线y=
,焦点在射线y=![]() (x≥0)上,且经过坐标原点.
(x≥0)上,且经过坐标原点.
(1)求抛物线的方程;
(2)设抛物线与x轴的另一个交点为B,P、Q为抛物线上两个动点,当点P在抛物线上运动时,如果使BP⊥PQ,求点Q的范围.
|
解析:(1)设抛物线的焦点坐标为(x0, 得| ∴焦点在F(1, 注意到抛物线过原点,则其开口向下,故所求抛物线方程为(x-1)2=-(y-1), 即:y=-x2+2x. (2)设P(α,-α2+2α),Q(β,-β2+2β)(α≠2,α≠β), 则:kBP= ∵BP⊥PQ,∴kBP·kPQ=-1. 即:-α[2-(α+β)]=-1, 亦即:α2+(β-2)α+1=0. 由Δ=(β-2)2-4≥0,得β≤0或β≥4. 故点Q存在范围是抛物线y=-x2+2x上x∈(-∞,0)∪[4,+∞). |


科目:高中数学 来源:2010-2011学年江苏省扬州中学高三模拟测试数学试卷(解析版) 题型:解答题
 -
-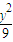 =l的一条渐近线的距离为3,则此抛物线的准线方程为 .
=l的一条渐近线的距离为3,则此抛物线的准线方程为 .查看答案和解析>>
科目:高中数学 来源:2010年江苏省南通市通州区高三回归课本专项检测数学试卷(解析版) 题型:解答题
 -
- =l的一条渐近线的距离为3,则此抛物线的准线方程为 .
=l的一条渐近线的距离为3,则此抛物线的准线方程为 .查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com