
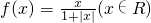 ,甲、乙、丙三位同学在研究此函数时分别给出命题:甲:函数f(x)的值域为(-1,1);乙:若x1≠x2则一定有f(x1)≠f(x2);丙:若规定
,甲、乙、丙三位同学在研究此函数时分别给出命题:甲:函数f(x)的值域为(-1,1);乙:若x1≠x2则一定有f(x1)≠f(x2);丙:若规定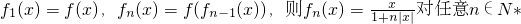 恒成立你认为上述三个命题中正确的个数有________.
恒成立你认为上述三个命题中正确的个数有________.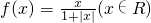 ,是一个奇函数,先研究自变量大于0时的性质,再由奇函数的性质导出另一部分的性质.甲研究的是其值域问题;乙研究的是单调性问题;丙研究的是一个恒等式,宜用递推关系推证结论.
,是一个奇函数,先研究自变量大于0时的性质,再由奇函数的性质导出另一部分的性质.甲研究的是其值域问题;乙研究的是单调性问题;丙研究的是一个恒等式,宜用递推关系推证结论.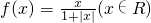 ,故函数是一个奇函数,先研究(0,+∞)上的性质
,故函数是一个奇函数,先研究(0,+∞)上的性质 即
即 ,函数在(0,+∞)上是增函数用值域为(0,1)
,函数在(0,+∞)上是增函数用值域为(0,1) ,
,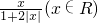 ,f3(x)=f(f2(x))=
,f3(x)=f(f2(x))=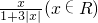 …fn(x)=f(fn-1(x))=
…fn(x)=f(fn-1(x))=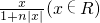 故丙也是正确的.
故丙也是正确的.

 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
| []x-1 |
| x |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 4 |
| 5 |
| 3 |
| 5 |
| 7 |
| 10 |
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com