
(2)������{an}���������n��N*����Sn=2an-n����f(x)=a1x+a2x2+��+anxn������f(x)��x=1���ĵ�����
(��)������{an}��ǰn���ΪSn����֪���������n��N*������Sn=2an-n��
(1)������{an}������a1�����ƹ�ϵʽ��an+1=f(an)��
(2)���Ķ�����Ķ�������������{an}�е��ƹ�ϵan+1=Aan+B������A��BΪ��������A��1��B��0��
������{an![]() }����AΪ���ȵĵȱ����С���������(1)�Ļ�����Ӧ�ñ�������������{an}��ͨ�ʽ��
}����AΪ���ȵĵȱ����С���������(1)�Ļ�����Ӧ�ñ�������������{an}��ͨ�ʽ��
(3)������{an}��ǰn���Sn��
�𰸣�(��)(1)an+1![]() =Aan+B
=Aan+B![]() =Aan
=Aan![]() =A(an
=A(an![]() )
)
A(an![]() )
)
��{an![]() }����AΪ���ȵĵȱ����У�
}����AΪ���ȵĵȱ����У�
(2)��Sn+1=2an+1-(n+1)��Sn=2an-n
��an+1=2an+1-2an-1
��an+1=2an+1
��(1)֪{an+1}�ǹ���Ϊ2�ĵȱ�����
��an=2n-1
��f��(x)=a1+2a2+3a3x2+��+nanxn-1
��f��(1)=a1+2a2+3a3+��+nan
=(2+2��22+3��23+��+n��2n)-(1+2+3+��+n)
=2+(n-2)2n+1![]()
(��)(1)��a1=2a1-1����a1=1
��Sn=2an-n ��
��Sn+1=2an+1-(n+1) ��
��-�ٵ�an+1=2an+1-2an-1
��an+1=2an+1��
(2)��an+1=2an+1
��{an+1}�ǵȱ����У�����Ϊ2������Ϊan+1=2
��an+1=2��2n-1����an=2n-1��
(3)Sn=(2-1)+(22-1)+(23-1)+��+(2n-1)
=(2+22+23+��+2n)-n=2n+1-2-n��


 �Ķ��쳵ϵ�д�
�Ķ��쳵ϵ�д�
| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
| ||
| a |
| ||
| x |
| 6 |
| 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ������ ���ͣ������
| ||
| a |
| ||
| x |
| 6 |
| 6 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2011��㶫ʡִ����ѧ�߶���ѧ�����п�����ѧ ���ͣ������
����С������14�֣� ��ͼ���ڳ�����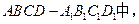
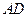
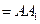
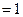
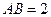
(1)֤��������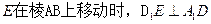 ;
;
(2)����������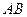 ���Ƿ���ڵ�
���Ƿ���ڵ�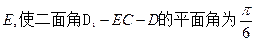 �������ڣ����
�������ڣ����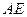 �ij����������ڣ���˵������.
�ij����������ڣ���˵������. 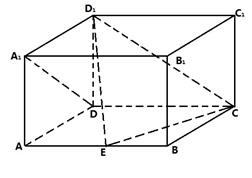
���ģ�����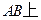
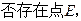 ʹ
ʹ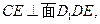 �����ڣ����
�����ڣ����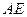 �ij����������ڣ���˵�����ɡ�
�ij����������ڣ���˵�����ɡ�
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ��2008-2009ѧ���Ĵ�ʡ�ɶ����и�����ѧר��ѵ����ָ�������������������棩 ���ͣ������
 ��a��0��a��1����
��a��0��a��1���� �ϵ����ݼ�����
�ϵ����ݼ����� �ϵ�����������a��ֵ��д�������Ľ���ʽ��
�ϵ�����������a��ֵ��д�������Ľ���ʽ���鿴�𰸺ͽ���>>
����ѧУ��ѡ - ��ϰ���б� - �����б�
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com