练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    已知点A(2，8)、B(x1，y1)、C(x2，y2)在抛物线y2=2px上，DABC的重心与此抛物线的焦点F重合，（1）写出该抛物线的方程和焦点F的坐标；（2）求线段BC中点M的坐标；（3）求BC所在直线的方程．

    答案：
    解析：

    		本小题主要考查直线、抛物线等基本知识，考查运用解析几何的方法分析问题和解决问题的能力．

    解：（1）由点A(2，8)在抛物线y2=2px上，有82=2p×2  解得p=16

    所以抛物线方程为y2=32x，焦点F的坐标为(8，0)

    （2）如图，由于F(8，0)是DABC的重心，M是BC的中点，所以F是线段AM的定比分点，且=2

    设点M的坐标为(x0，y0)，则

    解得x0=11，y0=-4

    所以点M的坐标为(11，-4)

    （3）由于线段BC的中点M不在x轴上，所以BC所在的直线不垂直于x轴．

    设BC所成直线的方程为：y+4=k(x-11)(k¹0)，

    由消x得ky2-32y-32(11k+4)=0，所以y1+y2=，由（2）的结论得

    =-4解得k=-4，因此BC所在直线的方程为：y+4=-4(x-11)，即4x+y-40=0．


    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：044

    已知点A(2，8)、B(x1，y1)、C(x2，y2)在抛物线y2=2px上，DABC的重心与此抛物线的焦点F重合，（1）写出该抛物线的方程和焦点F的坐标；（2）求线段BC中点M的坐标；（3）求BC所在直线的方程．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－1-1苏教版 苏教版 题型：044

    如图所示，已知点A(2，8)，B(x1，y1)，C(x2，y2)在抛物线y2＝2px上，△ABC的重心与此抛物线的焦点F重合．

    (1)写出该抛物线的方程和焦点F的坐标；

    (2)求线段BC中点M的坐标；

    (3)求BC所在直线的方程．

    查看答案和解析>>

    科目：高中数学 来源：遂宁高中高二第一学期期末检测数学试题(理科) 题型：044

    已知点A(2、8)，B(x1，y1)，C(x2，y2)在抛物线y2＝2Px上，△ABC的重心与抛物线的焦点F重合，如图：

    (1)写出该抛物线的方程和焦点坐标；

    (2)求线段BC中点M的坐标；

    (3)求BC所在直线方程．

    查看答案和解析>>

    科目：高中数学 来源：全优设计选修数学－2-1苏教版 苏教版 题型：044

    已知点A(2，8)，B(x1，y1)，C(x2，y2)在抛物线y2＝2px上，△ABC的重心与此抛物线的焦点F重合(如下图)．

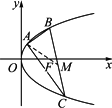
    (1)写出该抛物线的方程和焦点F的坐标；

    (2)求线段BC中点M的坐标．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    （08年唐山市一中调研一理） 已知点A(2，8)，在抛物线上，的重心与此抛物线的焦点F重合(如图).

       （I）写出该抛物线的方程和焦点F的坐标；

       （II）求线段BC中点M的坐标；   

       （III）求BC所在直线的方程.

     

    查看答案和解析>>

    同步练习册答案