
 |x|在x∈[-1,1]的图像上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m>
|x|在x∈[-1,1]的图像上有两点A、B,AB∥Ox轴,点M(1,m)(m∈R且m> )是△ABC的BC边的中点.
)是△ABC的BC边的中点. 
 t),A(-t,
t),A(-t, t)(t>0),C(x0,y0).
t)(t>0),C(x0,y0).  ∴
∴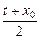 =1,
=1,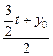 =m.
=m. t.
t.  t=2m-3t.
t=2m-3t. 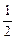 |AB|·hAB=
|AB|·hAB=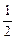 ·2t·(2m-3t),即f(t)=-3t2+2mt,t∈(0,1).
·2t·(2m-3t),即f(t)=-3t2+2mt,t∈(0,1). 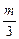 )2+
)2+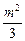 ,t∈(0,1
,t∈(0,1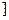 ,若
,若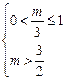 ,
, <m≤3,
<m≤3,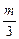 时,Smax=
时,Smax=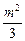 ,相应的C点坐标是(2-
,相应的C点坐标是(2-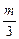 ,
, m),
m),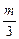 >1,即m>3
>1,即m>3 S=f(t)在区间(0,1]上是增函数,
S=f(t)在区间(0,1]上是增函数,

湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com