练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    过直线2x-y+4=0与x-y+5=0的交点，且垂直于直线x-2y=0的直线方程是（ ）
    A．2x+y-8=0
    B．2x-y-8=0
    C．2x+y+8=0
    D．2x-y+8=0
    【答案】分析：设过直线2x-y+4=0与x-y+5=0的交点的直线方程为2x-y+4+λ（x-y+5）=0，依题意可求其斜率k=-2，从而可求得λ．
    解答：解：设过直线2x-y+4=0与x-y+5=0的交点的直线方程为2x-y+4+λ（x-y+5）=0，
    即（2+λ）x-（1+λ）y+4+5λ=0，
    ∵该直线与直线x-2y=0垂直，
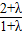
    ∴k==-2，
    ∴λ=-．
    ∴所求的直线方程为：（2-）x-（1-）y+4+5×（-）=0，
    即2x+y-8=0．
    故选A．
    点评：本题考查直线的一般式方程与直线的垂直关系，考查直线系方程的应用，属于中档题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    过直线2x-y+4=0与x-y+5=0的交点，且垂直于直线x-2y=0的直线方程是（　　）

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点，且满足下列条件之一的圆的方程：
    （1）过原点；        
    （2）有最小面积．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知圆C过直线2x+y+4=0 和圆x2+y2+2x-4y+1=0的交点，且原点在圆C上．则圆C的方程为
    x2+y2+
    3
    2
    x-
    17
    4
    y=0
    x2+y2+
    3
    2
    x-
    17
    4
    y=0
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    过直线2x+y+4=0与x2+y2+2x-4y+1=0有交点的圆，并且面积最小，满足此条件的圆的方程为
     
    ．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    求过直线2x+y+4=0和圆x2+y2+2x-4y+1=0的交点，且满足下列条件之一的圆的方程.

    (1)过原点;

    (2)有最小面积.

    查看答案和解析>>

    同步练习册答案