
在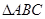 中,
中,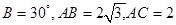 。求
。求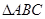 的面积
的面积
【解析】
【错解分析】根据三角形面积公式,只需利用正弦定理确定三角形的内角C,则相应的三角形内角A即可确定再利用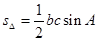 即可求得。但由于正弦函数在区间
即可求得。但由于正弦函数在区间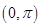 内不严格格单调所以满足条件的角可能不唯一,这时要借助已知条件加以检验,务必做到不漏解、不多解。
内不严格格单调所以满足条件的角可能不唯一,这时要借助已知条件加以检验,务必做到不漏解、不多解。
【正解】根据正弦定理知: 即
即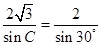 得
得 ,
,
由于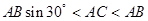 即满足条件的三角形有两个
即满足条件的三角形有两个
故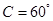 或
或 .则
.则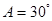 或
或
故相应的三角形面积为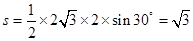 或
或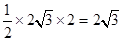 .
.
【点评】正弦定理和余弦定理是解三角形的两个重要工具,它沟通了三角形中的边角之间的内在联系,正弦定理能够解决两类问题(1)已知两角及其一边,求其它的边和角。这时有且只有一解。(2)已知两边和其中一边的对角,求其它的边和角,这是由于正弦函数在在区间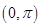 内不严格格单调,此时三角形解的情况可能是无解、一解、两解,可通过几何法来作出判断三角形解的个数。
内不严格格单调,此时三角形解的情况可能是无解、一解、两解,可通过几何法来作出判断三角形解的个数。


 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com