
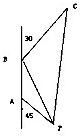
 某油轮以30海里/小时的速度航行,在A点测得海面上油井P在南偏东45°,向北航行40分钟后到达B点,测得海面上油井P在南偏东15°,油轮改为北偏东30°的航向再行驶80分钟到达C点,求PC间的距离.
某油轮以30海里/小时的速度航行,在A点测得海面上油井P在南偏东45°,向北航行40分钟后到达B点,测得海面上油井P在南偏东15°,油轮改为北偏东30°的航向再行驶80分钟到达C点,求PC间的距离.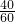 =20,BC=30×
=20,BC=30×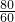 =40,
=40,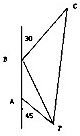
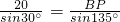 ,
,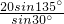 =20
=20 .(4分)
.(4分)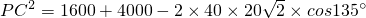 =4000.
=4000. 海里.(8分)
海里.(8分) 海里.(9分)
海里.(9分) .在△CBP中,∠CBP=135°,由余弦定理,能求出PC间的距离.
.在△CBP中,∠CBP=135°,由余弦定理,能求出PC间的距离.

科目:高中数学 来源: 题型:
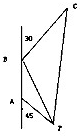 某油轮以30海里/小时的速度航行,在A点测得海面上油井P在南偏东45°,向北航行40分钟后到达B点,测得海面上油井P在南偏东15°,油轮改为北偏东30°的航向再行驶80分钟到达C点,求PC间的距离.
某油轮以30海里/小时的速度航行,在A点测得海面上油井P在南偏东45°,向北航行40分钟后到达B点,测得海面上油井P在南偏东15°,油轮改为北偏东30°的航向再行驶80分钟到达C点,求PC间的距离.查看答案和解析>>
科目:高中数学 来源:山东省高密市2011-2012学年高二10月月考数学文科试题 题型:044
如下图所示,某海轮以30海里/小时的速度航行,在A点测得海面上油井P在南偏东60°,向北航行40分钟后到达B点,测得油井P在南偏东30°,海轮改为北偏东60°的航向再行驶80分钟到达C点,求P,C间的距离.
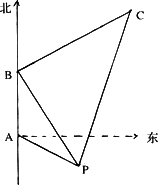
查看答案和解析>>
科目:高中数学 来源:山东省宁阳四中2011-2012学年高二上学期期中学分认定数学文科试题(人教版) 人教版 题型:044
如下图所示,某海轮以30海里/小时的速度航行,在A点测得海面上油井P在南偏东60°,向北航行40分钟后到达B点,测得油井P在南偏东30°,海轮改为北偏东60°的航向再行驶80分钟到达C点,求P,C间的距离.
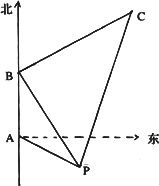
查看答案和解析>>
科目:高中数学 来源:同步题 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com