
如图,已知点M在菱形ABCD的BC边上,连结AM交BD于点E,过菱形ABCD的顶点C作CN∥AM,分别交BD、AD于点F、N,连结AF、CE.判断四边形AECF的形状,并说明理由.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案科目:高中数学 来源: 题型:
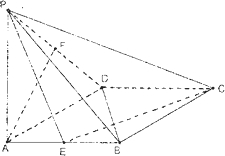 如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB与PD的中点.
如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB与PD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
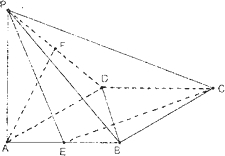 如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB与PD的中点.
如图,已知:在菱形ABCD中,∠DAB=60°,PA⊥底面ABCD,PA=DA,E,F分别是AB与PD的中点.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省无锡市江阴市成化高中高三(上)第一次段考数学试卷(文理合卷)(解析版) 题型:解答题
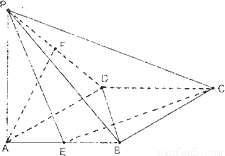
查看答案和解析>>
科目:高中数学 来源: 题型:
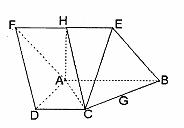
如图已知:菱形ABEF所在平面与直角梯形ABCD所在平面互相垂直,AB=2AD=2CD=4,∠ABE=60°,∠BAD=∠CDA=90°点H,G分别是线段EF,BC的中点.
(1)求证:平面AHC⊥平面BCE:
(2)试问在线段EF上是否存在点M,使得MG//平面AFD,若存在求FM的长并证明;若不存在,说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com