设常数a∈R,以方程|x+a|•2x=2011的根的可能个数为元素的集合A= .
【答案】
分析:因为方程|x+a|•2
x=2011的根的个数,可以转化为对应函数图象交点的个数,所以可以借助于图形求解画出函数的图象即可得到答案..
解答:解:因为 方程|x+a|•2
x=2011的根个数就是函数y=|x+a|,y=2011×2
-x交点个数,画出对应图象得
①当a非常小即y=|x+a|的图象在y轴右侧,且离y轴很远时,交点有2个;

②当a非常大即y=|x+a|的图象在y轴左侧,且离y轴很远时,因为指数函数的递增递减较快,故交点有3个.
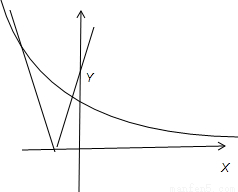
即集合A={1,2,3}
故答案为 {1,2,3}.
点评:本题主要考查根的个数判断问题.因为方程根的个数可以转化为对应函数图象的交点个数,所以通常借助与图形求解.




