A
分析:通过分三种类型:第一类:先排没有限制条件的3人,再用“插空法”排A、B、C,最后用“插空法”排D、E;第二类:先排没有限制条件的3人(设为F、G、H),再将A、B、C中选两个捆在一起,把捆在一起的两人看作一人和另外一人用“插空法”排在四个空隙中,然后从D、E中选一个放在捆在一起的两元素之间,最后一个元素安排在剩余的6个空隙中; 第三类:先排没有限制条件的3人(设为F、G、H),再把A、B、C三个人“捆绑”在一起,看作一个元素安排在四个空隙中,然后再把D、E利用“插空法”安排在A、B、C之间的两个空隙中,即可求解.
解答:分三类:第一类:先排没有限制条件的3人(设为F、G、H),有

种,再用“插空法”排A、B、C,有
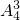
种,最后用“插空法”排D、E,有
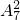
种,∴第一类共有

•
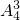
•
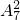
=6 048种排法.
第二类:先排没有限制条件的3人(设为F、G、H),有

种,再将A、B、C中选两个捆在一起有

种捆法,把捆在一起的两人看作一人和另外一人用“插空法”排在四个空隙中,有
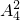
种排法,然后从D、E中选一个放在捆在一起的两元素之间有
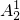
种方法,最后一个元素安排在剩余的6个空隙中有
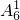
种方法,故第二类共有

•

•
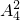
•
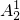
•
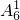
=5 184种排法.
第三类:先排没有限制条件的3人(设为F、G、H),有

种排法,再把A、B、C三个人“捆绑”在一起有

种“捆法”,看作一个元素安排在四个空隙中,有
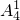
种放法,然后再把D、E利用“插空法”安排在A、B、C之间的两个空隙中,有

种方法,故第三类共有

•

•
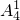
•

=288种方法.
综上所述,符合条件的所有排法共有6 048+5 184+288=11520种.
故选A.
点评:本题考查排列组合的简单应用,利用分类计数原理以及分步计数原理,做到不重复不要漏,题目难度较大.

 种,再用“插空法”排A、B、C,有
种,再用“插空法”排A、B、C,有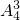 种,最后用“插空法”排D、E,有
种,最后用“插空法”排D、E,有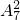 种,∴第一类共有
种,∴第一类共有 •
•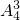 •
•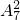 =6 048种排法.
=6 048种排法. 种,再将A、B、C中选两个捆在一起有
种,再将A、B、C中选两个捆在一起有 种捆法,把捆在一起的两人看作一人和另外一人用“插空法”排在四个空隙中,有
种捆法,把捆在一起的两人看作一人和另外一人用“插空法”排在四个空隙中,有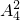 种排法,然后从D、E中选一个放在捆在一起的两元素之间有
种排法,然后从D、E中选一个放在捆在一起的两元素之间有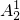 种方法,最后一个元素安排在剩余的6个空隙中有
种方法,最后一个元素安排在剩余的6个空隙中有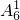 种方法,故第二类共有
种方法,故第二类共有 •
• •
•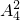 •
•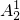 •
•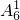 =5 184种排法.
=5 184种排法. 种排法,再把A、B、C三个人“捆绑”在一起有
种排法,再把A、B、C三个人“捆绑”在一起有 种“捆法”,看作一个元素安排在四个空隙中,有
种“捆法”,看作一个元素安排在四个空隙中,有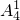 种放法,然后再把D、E利用“插空法”安排在A、B、C之间的两个空隙中,有
种放法,然后再把D、E利用“插空法”安排在A、B、C之间的两个空隙中,有 种方法,故第三类共有
种方法,故第三类共有 •
• •
•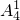 •
• =288种方法.
=288种方法.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案