�⣺��1����x
1=x
2=0?f��x
0��=-f��0��������x
1=1��x
2=0��f��1��=-f��0����
��f��x
0��=f��1�����ɺ���f��x��������֪��x
0=1��
��2���ɣ�1��֪��f��x
1+x
2��=f��x
1��+f��x
2��+f��1��=f��x
1��+f��x
2��+1��
��x
1��x
2�������ԣ���x
1=n��x
2=1��f��n+1��=f��n��+f��1��+1=f��n��+2��
��f��n��=2n-1����n��N
*����
��
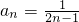
��
�֡�
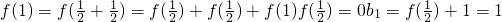
��
�֡�
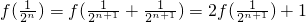
��
��
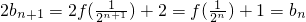
��
��
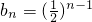
��
��������ͷ���֪��
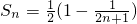
��
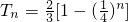
����
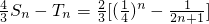
��
��4
n=��3+1��
n=C
nn3
n+C
nn-13
n-1+��+C
n13+C
n0��3n+1��2n+1����
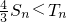
��
��3����F��n��=a
n+1+a
n+2+��+a
2n?F��n+1��-F��n��=a
2n+1+a
2n+2-a
n+1=
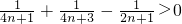
��ͨ����֤���൱n��2ʱ��
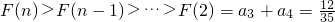
��
��
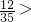
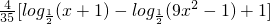
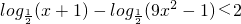
��
��˲���ʽ������x��ȡֵ��ΧΪ
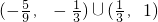
��
��������1���ֱ���x
1=x
2=0��x
1=1��x
2=0��f��x
0��=f��1��������Ϊf��x��Ϊ�����������Ӷ�����x
0��ֵ��
��2���ɣ�1����f��x
1+x
2��=f��x
1��+f��x
2��+1������x
1=n��x
2=1��f��n+1��=f��n��+f��1��+1=f��n��+2��f��n��=2n-1���ʿ���a
n��������
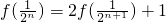
���Ӷ�����ͨ��ʿ�֤��
��3�����캯��F��n��=a
n+1+a
n+2+��+a
2n��֤��n��2ʱ��Ϊ�������������Ӷ�����x��ȡֵ��Χ��
�������������¶���Ϊ���壬��������������鸳ֵ����ͬʱ���鹹�캯�������ú����ĵ����Խ����������⣮

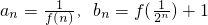 ����Sn=a1a2+a2a3+��+anan+1��Tn=b1b2+b2b3+��+bnbn+1���Ƚ�
����Sn=a1a2+a2a3+��+anan+1��Tn=b1b2+b2b3+��+bnbn+1���Ƚ�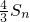 ��Tn�Ĵ�С��ϵ��������֤����
��Tn�Ĵ�С��ϵ��������֤����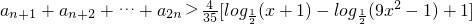 ������
������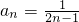 ��
��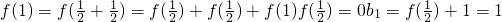 ��
��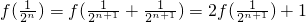 ��
��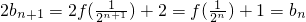 ��
��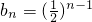 ��
��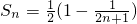 ��
��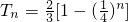 ����
����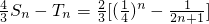 ��
��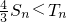 ��
��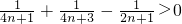 ��ͨ����֤���൱n��2ʱ��
��ͨ����֤���൱n��2ʱ��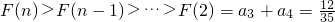 ��
��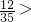
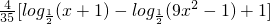
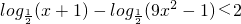 ��
��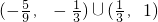 ��
��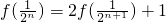 ���Ӷ�����ͨ��ʿ�֤��
���Ӷ�����ͨ��ʿ�֤��

 ��У����ϵ�д�
��У����ϵ�д�