
下表所示为X、Y、Z三种食物的维生素含量及其成本.

某人欲将这三种食物混合,制成100 kg的混合物,设所用的食物X、Y、Z的份量依次是x,y,z(kg).
(1)试以x,y表示z;
(2)试以x,y表示混合物成本;
(3)若混合物至少需要44 000单位维生素A及48 000单位维生素B,证明y≥20,2x-y≥40,x+y≤100;
(4)确定使成本最少的x,y,z的值.
(1)x+y+z=100,所以z=100-x-y.
(2)混合物成本Q=6x+5y+4z=6x+5y+4(100-x-y)=400+2x+y.
(3)因为400x+600y+400z≥44000,即400x+600y+400(100-x-y)≥44000,所以y≥20.因为800x+200y+400z≥48000,即800x+200y+400(100-x-y)≥48000,所以2x-y≥40.因为x+y+z=100,所以x+y=100-z.而z≥0,所以x+y≤100.
(4)作出不等式组所表示的平面区域(如图),

 目标函数为P=40+2x+y.当点(x,y)在平面区域△ABC(包括边界)上变动时,目标函数P在点A(30,20)处取得最小值480.
目标函数为P=40+2x+y.当点(x,y)在平面区域△ABC(包括边界)上变动时,目标函数P在点A(30,20)处取得最小值480.
在第(4)问中,可以将z用x和y来表示,从而达到减少变量的效果.


 100分闯关期末冲刺系列答案
100分闯关期末冲刺系列答案科目:高中数学 来源: 题型:
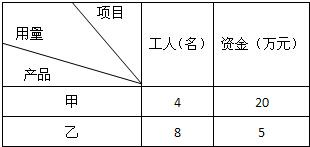 某工厂生产甲、乙两种产品,每种产品都有一部分是一等品,其余是二等品,已知甲产品为一等品的概率比乙产品为一等品的概率多0.25,甲产品为二等品的概率比乙产品为一等品的概率少0.05
某工厂生产甲、乙两种产品,每种产品都有一部分是一等品,其余是二等品,已知甲产品为一等品的概率比乙产品为一等品的概率多0.25,甲产品为二等品的概率比乙产品为一等品的概率少0.05查看答案和解析>>
科目:高中数学 来源:辽宁省高考真题 题型:解答题


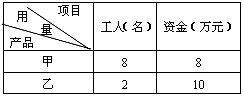
查看答案和解析>>
科目:高中数学 来源:2010年广东省茂名市高考数学一模试卷(文科)(解析版) 题型:解答题

查看答案和解析>>
科目:高中数学 来源:2010年广东省高考各地一模试卷汇集02:概率和统计(解析版) 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com