
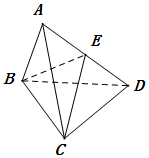
 如图所示,△ABC和△BCD都是边长为2的正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是边长为2的正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.分析 (1)设BC的中点为O,连AO、DO,可证AO⊥平面BCD,求得$AO=\sqrt{3}$,又E为AD中点,可求E点到平面BCD的距离,由三角形面积公式求得△BDC的面积,利用三棱锥的体积公式即可计算得解.
(2)由(1)可求$AO=DO=\sqrt{3}$,进而可求AD,由CA=CD,E为AD中点,可求CE,同理可求BE,进而通过BC2≠BE2+CE2,证明直线CE与平面ABD是不垂直.
解答 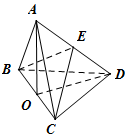 (本题满分为12分)
(本题满分为12分)
解:(1)设BC的中点为O,连AO、DO.
由AB=AC,则AO⊥BC,
由平面ABC⊥平面BCD,BC是它们的交线知:AO⊥平面BCD,
由已知得$AO=\sqrt{3}$,…(2分)
即A点到平面BCD的距离为$\sqrt{3}$,
又E为AD中点,
则E点到平面BCD的距离为$\frac{{\sqrt{3}}}{2}$,
而△BDC的面积为$\sqrt{3}$,
故${V_{三棱锥E-BCD}}=\frac{1}{3}×\frac{{\sqrt{3}}}{2}×\sqrt{3}=\frac{1}{2}$. …(6分)
(2)直线CE与平面ABD是不垂直.…(8分)
理由如下:假设直线CE与平面ABD垂直,
由(1)知∠AOD=90°,且$AO=DO=\sqrt{3}$,
则$AD=\sqrt{A{O^2}+D{O^2}}=\sqrt{6}$,
由CA=CD,E为AD中点,
则$CE=\sqrt{A{C^2}-A{E^2}}=\frac{{\sqrt{10}}}{2}$,同理可得$BE=\frac{{\sqrt{10}}}{2}$,
若CE⊥平面ABD,BE?平面ABD,
则CE⊥BE,应有BC2=BE2+CE2,
而BC2=4,$B{E^2}+C{E^2}={(\frac{{\sqrt{10}}}{2})^2}+{(\frac{{\sqrt{10}}}{2})^2}=5$,
则BC2≠BE2+CE2,这与假设矛盾,假设不成立.
故直线CE与平面ABD是不垂直. …(12分)
点评 本题主要考查了直线与平面垂直的判定,棱锥的体积的求法,考查了数形结合思想,空间想象能力和推理论证能力,属于中档题.


科目:高中数学 来源: 题型:解答题
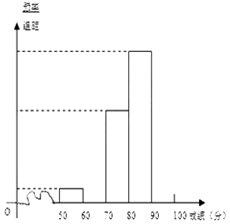 中日“钓鱼岛争端”问题越来越引起社会关注,我校对高二600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.
中日“钓鱼岛争端”问题越来越引起社会关注,我校对高二600名学生进行了一次“钓鱼岛”知识测试,并从中抽取了部分学生的成绩(满分100分)作为样本,绘制了下面尚未完成的频率分布表和频率分布直方图.| 分 组 | 频 数 | 频 率 |
| [50,60) | 2 | 0.04 |
| [60,70) | 8 | 0.16 |
| [70,80) | 10 | 0.2 |
| [80,90) | 16 | 0.32 |
| [90,100] | 14 | 0.28 |
| 合 计 | 50 | 1.00 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 若p:?x∈R,x2+3x+5>0,则¬p:?x0∈R,x02+3x0+5<0 | |
| B. | “若α=$\frac{π}{3}$,则cosα=$\frac{1}{2}$”的否命题是“若α=$\frac{π}{3}$,则cosα≠$\frac{1}{2}$” | |
| C. | 已知A,B是△ABC的两个内角,则“A>B”是“sinA>sinB”的充要条件 | |
| D. | 命题“p∨q为真”是命题“p∧q为真”的充分不必要条件 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{π}{6}$ | B. | $\frac{π}{2}$ | C. | $\frac{π}{16}$ | D. | $\frac{π}{4}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $\frac{8}{5}$ | B. | $\frac{4}{5}$ | C. | $\frac{4}{3}$ | D. | $\frac{3}{2}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
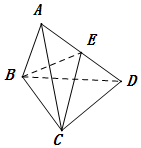 如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.
如图所示,△ABC和△BCD都是正三角形,平面ABC⊥平面BCD,连接AD,E是线段AD的中点.查看答案和解析>>
科目:高中数学 来源: 题型:解答题
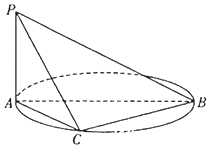 如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.
如图,AB是圆O的直径,PA垂直圆所在的平面,C是圆上的点.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com