
如图,四棱锥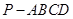 的底面是正方形,
的底面是正方形,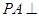 底面
底面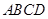 ,
, ,
,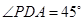 ,点
,点 、
、 分别为棱
分别为棱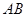 、
、 的中点.
的中点.

(1)求证: 平面
平面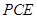 ;
;
(2)求证:平面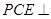 平面
平面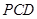 ;
;
(3)求三棱锥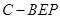 的体积.
的体积.
(1)详见解析;(2)详见解析;(3)三棱锥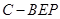 的体积为
的体积为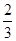 .
.
【解析】
试题分析:(1)取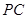 的中点
的中点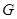 ,连接
,连接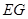 、
、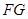 ,证明四边形
,证明四边形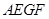 为平行四边形,得到
为平行四边形,得到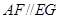 ,再利用直线平面平行的判定定理得到
,再利用直线平面平行的判定定理得到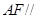 平面
平面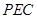 ;(2)先证明
;(2)先证明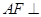 平面
平面 ,利用(1)中的条件
,利用(1)中的条件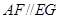 得到
得到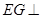 平面
平面 ,再利用平面与平面垂直的判定定理证明平面
,再利用平面与平面垂直的判定定理证明平面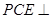 平面
平面 ,在证明
,在证明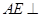 平面
平面 的过程中,在等腰三角形
的过程中,在等腰三角形 中利用三线合一得到
中利用三线合一得到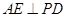 ,通过证明
,通过证明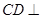 平面
平面 得到
得到 ,然后利用直线与平面垂直的判定定理即可证明
,然后利用直线与平面垂直的判定定理即可证明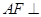 平面
平面 ;(3)利用题中的条件
;(3)利用题中的条件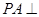 平面
平面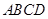 ,在计算三棱锥
,在计算三棱锥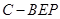 的体积中,选择以点
的体积中,选择以点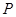 为顶点,
为顶点,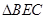 所在平面为底面的三棱锥来计算其体积,则该三棱锥的高为
所在平面为底面的三棱锥来计算其体积,则该三棱锥的高为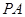 ,最后利用锥体的体积计算公式即可.
,最后利用锥体的体积计算公式即可.
试题解析:(1)取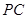 的中点
的中点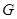 ,连结
,连结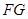 、
、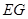 ,
,
∴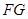 为
为 的中位线,
的中位线,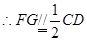 ,
,
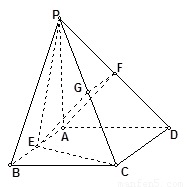
∵四边形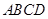 为矩形,
为矩形,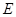 为
为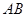 的中点,
的中点,
∴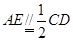 ,
, ,
,
∴四边形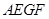 是平行四边形,
是平行四边形,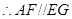 ,
,
又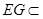 平面
平面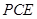 ,
,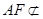 平面
平面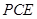 ,
,
∴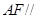 平面
平面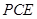 ;
;
(2) 底面
底面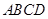 ,
,
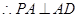 ,
,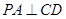 ,又
,又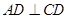 ,
,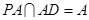 ,
,
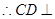 平面
平面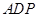 ,
又
,
又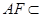 平面
平面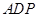 ,
,
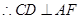 ,
,
直角三角形 中,
中,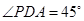 ,
,
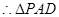 为等腰直角三角形,
为等腰直角三角形,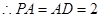 ,
,
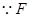 是
是 的中点,
的中点,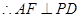 ,又
,又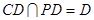 ,
,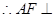 平面
平面 ,
,
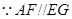 ,
, 平面
平面 ,
,
又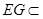 平面
平面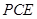 ,
平面
,
平面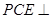 平面
平面 ;
;
(3)三棱锥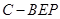 即为三棱锥
即为三棱锥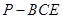 ,
,
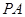 是三棱锥
是三棱锥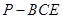 的高,
的高,
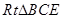 中,
中,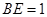 ,
,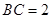 ,
,
 三棱锥
三棱锥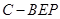 的体积,
的体积,
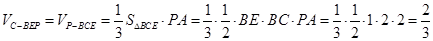 .
.
考点:1.直线与平面平行;2.平面与平面垂直;3.等体积法求三棱锥的体积


科目:高中数学 来源: 题型:
(09年山东实验中学诊断三理)(13分)如图:四棱锥![]() 的底面
的底面![]() 是提醒,腰
是提醒,腰![]() ,
,![]() 平分
平分![]() 且与
且与![]() 垂直,侧面
垂直,侧面![]() 都垂直于底面,平面
都垂直于底面,平面![]() 与底面
与底面![]() 成60°角
成60°角
![]() (1)求证:
(1)求证:![]() ;
;
![]() (2)求二面角
(2)求二面角![]() 的大小
的大小![]()
![]()
![]()
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省高三第八次月考文科数学试卷 题型:解答题
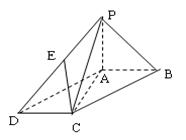
如图,四棱锥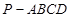 的底面是平行四边形,
的底面是平行四边形,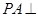 平面
平面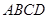 ,
,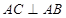 ,
,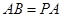 ,
,
点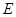 是
是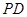 上的点,且
上的点,且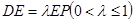 .
.
(Ⅰ)求证: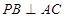 ;
;
(Ⅱ)求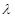 的值,使
的值,使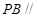 平面
平面 ;
;
(Ⅲ)当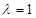 时,求三棱锥
时,求三棱锥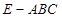 与四棱锥
与四棱锥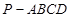 的体积之比.
的体积之比.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年浙江省高三上学期摸底理科数学 题型:解答题
((本小题满分14分)如图,四棱锥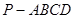 的底面
的底面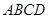 是正方形,侧棱
是正方形,侧棱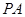
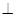 底面
底面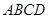 ,
,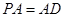 ,
,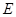 、
、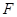 分别是棱
分别是棱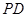 、
、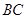 的中点.
的中点.
(1)求证: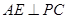 ; (2) 求直线
; (2) 求直线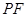 与平面
与平面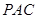 所成的角的正切值
所成的角的正切值
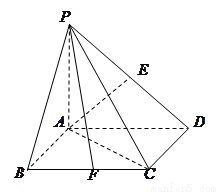
查看答案和解析>>
科目:高中数学 来源:2010-2011年四川省成都市高二3月月考数学试卷 题型:填空题
(本小题满分12 分)
如图,四棱锥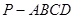 的底面是边长为
的底面是边长为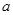 的菱形,
的菱形,
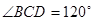 ,
,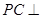 平面
平面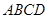 ,
,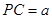 ,
,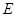 为
为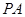 的中点,O为底面对角线的交点;
的中点,O为底面对角线的交点;
(1)求证:平面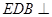 平面
平面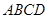 ;
;
(2)求二面角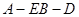 的正切值。
的正切值。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com