练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    若tanα=2，则sinαcosα的值为（ ）
    A．
    B．-
    C．
    D．
    【答案】分析：由同角三角函数的商数关系，结合tanα=2得sinα=2cosα，再由平方关系算出cos2α=，从而得到sinαcosα=2cos2α=．
    解答：解：∵tanα=2，
    ∴=2，得sinα=2cosα
    又∵sin2α+cos2α=1
    ∴4cos2α+cos2α=1，得cos2α=
    因此，sinαcosα=2cos2α=
    故选：A
    点评：本题给出角的正切值，求它的正弦与余弦的积，着重考查了运用同角三角函数的关系求值的知识，属于基础题．
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    下列命题错误的是（　　）

    查看答案和解析>>

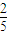
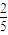
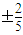
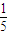
    科目：高中数学 来源：河北省秦皇岛一中2008-2009学年高二下学期第三次月考数学试题(理科) 题型：013

    已知△ABC的三个内角A、B、C所对的三边分别为a、b、c，若△ABC的面积S＝c2－(a－b)2，则tan等于

    [　　]

    A．

    B．

    C．

    D．1

    查看答案和解析>>

    科目：高中数学 来源：天利38套《2008全国各省市高考模拟试题汇编(大纲版)》、数学理 题型：013

    已知△ABC的三个内角A、B、C所对的三边分别为a、b、c，若△ABC的面积S＝c2－(a－b)2，则tan等于

    [　　]

    A．

    B．

    C．

    D．1

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知△ABC的三个内角为A、B、C,所对的三边为a、b、c,若△ABC的面积为S=a2-(b-c)2,则tan=       .

    查看答案和解析>>

    科目：高中数学 来源：2011-2012学年山东省德州市乐陵一中高三（上）期末数学复习训练试卷7（解析版） 题型：选择题

    下列命题错误的是（ ）
    A．对于等比数列{an}而言，若m+n=k+S，m、n、k、S∈N*，则有am•an=ak•aS
    B．点（-，0）为函数f（x）=tan（2x+）的一个对称中心
    C．若||=1，||=2，向量与向量的夹角为120°，则在向量上的投影为1
    D．“sinα=sinβ”的充要条件是“α+β=（2k+1）π或α-β=2kπ （k∈Z）”

    查看答案和解析>>

    同步练习册答案