Question

（04年福建卷理）（12分）

如图，P是抛物线C：y=x²上一点，直线l过点P且与抛物线C交于另一点Q.

（Ⅰ）若直线l与过点P的切线垂直，求线段PQ中点M的轨迹方程；

（Ⅱ）若直线l不过原点且与x轴交于点S，与y轴交于点T，试求的取值范围.

Answer 1

解析：（Ⅰ）设P(x₁，y₁)，Q(x₂，y₂)，M(x₀，y₀)，依题意x₁≠0，y₁>0，y₂>0.

由y=x²，           ①

得y＇=x.

∴过点P的切线的斜率k_切= x₁，

∴直线l的斜率k_l=-=-，

∴直线l的方程为y-x₁²=- (x-x₁)，

方法一：

联立①②消去y，得x²+x-x₁²-2=0.

∵M是PQ的中点

∴

消去x₁，得y₀=x₀²++1(x₀≠0)，

∴PQ中点M的轨迹方程为y=x²++1(x≠0).

方法二：

由y₁=x₁²，y₂=x₂²，x₀=，

得y₁-y₂=x₁²-x₂²=(x₁+x₂)(x₁-x₂)=x₀(x₁-x₂)，

则x₀==k_l=-，

∴x₁=-，

将上式代入②并整理，得

y₀=x₀²++1(x₀≠0)，

∴PQ中点M的轨迹方程为y=x²++1(x≠0).

（Ⅱ）设直线l:y=kx+b，依题意k≠0，b≠0，则T(0，b).

分别过P、Q作PP＇⊥x轴，QQ＇⊥y轴，垂足分别为P＇、Q＇，则

.

由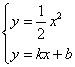消去x，得y²-2(k²+b)y+b²=0.      ③

则

方法一：

∴|b|()≥2|b|=2|b|=2.

∵y₁、y₂可取一切不相等的正数，

∴的取值范围是（2，+）.

方法二：

∴=|b|=|b|.

当b>0时，=b==+2>2；

当b<0时，=-b=.

又由方程③有两个相异实根，得△=4(k²+b)²-4b²=4k²(k²+2b)>0，

于是k²+2b>0，即k²>-2b.

所以>=2.

∵当b>0时，可取一切正数，

∴的取值范围是（2，+）.

方法三：

由P、Q、T三点共线得k_TQ=K_TP，

即=.

则x₁y₂-bx₁=x₂y₁-bx₂，即b(x₂-x₁)=(x₂y₁-x₁y₂).

于是b==-x₁x₂.

∴==+=+≥2.

∵可取一切不等于1的正数，

∴的取值范围是（2，+）.