
某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.

(1)设AB=x米,cosA=f(x),求f(x)的解析式,并指出x的取值范围;
(2)求四边形ABCD面积的最大值.
|
解:(1)在△ABD中,由余弦定理得 BD2=AB2+AD2-2AB·AD·cosA. 同理,在△CBD中,BD2=CB2+CD2-2CB·CD·cosC.2分 因为∠A和∠C互补, 所以AB2+AD2-2AB·AD·cosA=CB2+CD2-2CB·CD·cosC =CB2+CD2+2CB·CD·cosA.4分 即 x2+(9-x)2-2 x(9-x) cosA=x2+(5-x)2+2 x(5-x) cosA. 解得cosA= (2)四边形ABCD的面积
S= =x(7-x) 记g(x)=(x2-4)(x2-14x+49),x∈(2,5). 由g′(x)=2x(x2-14x+49)+(x2-4)(2 x-14)=2(x-7)(2 x2-7 x-4)=0, 解得x=4(x=7和x=- 所以函数g(x)在区间(2,4)内单调递增,在区间(4,5)内单调递减.11分 因此g(x)的最大值为g(4)=12×9=108. 所以S的最大值为 答:所求四边形ABCD面积的最大值为6 |


科目:高中数学 来源: 题型:
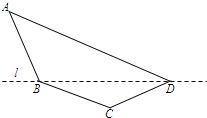 (2012•南京二模)某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
(2012•南京二模)某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.查看答案和解析>>
科目:高中数学 来源:2013年高考数学复习卷B(二)(解析版) 题型:解答题
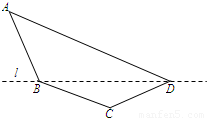 某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.查看答案和解析>>
科目:高中数学 来源:2012年江苏省南京市高考数学二模试卷(解析版) 题型:解答题
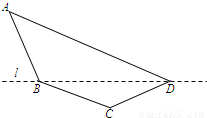 某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.查看答案和解析>>
科目:高中数学 来源:2012年安徽省蚌埠二中高考数学一模试卷(文科)(解析版) 题型:解答题
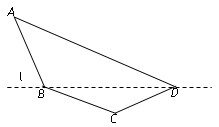
 某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.
某单位设计一个展览沙盘,现欲在沙盘平面内,布设一个对角线在l上的四边形电气线路,如图所示.为充分利用现有材料,边BC,CD用一根5米长的材料弯折而成,边BA,AD用一根9米长的材料弯折而成,要求∠A和∠C互补,且AB=BC.查看答案和解析>>
科目:高中数学 来源:安徽省模拟题 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com