练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    已知y＝f(x)是函数的反函数，

    (Ⅰ)解关于x的不等式：1＝ef(x)＋g(x)＞0；

    (Ⅱ)当a＝1时，过点(1，－1)是否存在函数y＝f(x)图象的切线？若存在，有多少条？若不存在，说明理由；

    (Ⅲ)．若a是使f(x)≥g(x)(x≥1)恒成立的最小值，试比较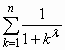与f[(1＋n)λ2n(1－λ)]的大小(0＜λ＜1，n∈N*)．

    答案：
    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源：安徽省合肥八中2012届高三第三次段考数学文科试题 题型：013

    已知函y＝f(x)定义在[－，]上，且其导函数的图象如图所示，则函数y＝f(x)可能是

    [　　]
    A．

    y＝sinx

    B．

    y＝－sinx·cosx

    C．

    y＝sinx·cosx

    D．

    y＝cosx

    查看答案和解析>>

    科目：高中数学 来源：新课标2012届高三下学期二轮复习综合验收(5)数学理科试题 题型：013

    已知函教f(x)＝Asin(ωx＋φ)(A＞0，ω＞0)的图象与直线y＝b(0＜b＜A)的三个相邻交点的横坐标分别是2，4，8，则f(x)的单调递增区间是

    [　　]

    A．[6kπ，6kπ＋3]，k∈Z

    B．[6k－3，6k]，k∈Z

    C．[6k，6k＋3]，k∈Z

    D．[6kπ－3，6kπ]，k∈Z

    查看答案和解析>>

    科目：高中数学 来源：河南省郑州外国语学校2012届高三下学期综合测试验收(5)数学文科试题 题型：013

    已知函教f(x)＝Asin(ωx＋)(A＞0，ω＞0)的图象与直线y＝b(0＜b＜A)的三个相邻交点的横坐标分别是2，4，8，则f(x)的单调递增区间是

    [　　]

    A．[6kπ，6kπ＋3]，k∈Z

    B．[6k－3，6k]，k∈Z

    C．[6k，6k＋3]，k∈Z

    D．[6kπ－3，6kπ]，k∈Z

    查看答案和解析>>

    科目：高中数学 来源：河南省郑州外国语学校2012届高三下学期综合测试验收(5)数学理科试题 题型：013

    已知函教f(x)＝Asin(ωx＋φ)(A＞0，ω＞0)的图象与直线y＝b(0＜b＜A)的三个相邻交点的横坐标分别是2，4，8，则f(x)的单调递增区间是

    [　　]

    A．[6kπ，6kπ＋3]，k∈Z

    B．[6k－3，6k]，k∈Z

    C．[6k，6k＋3]，k∈Z

    D．[6kπ－3，6kπ]，k∈Z

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    已知函数f(x)＝a－是偶函数，a为实常数.

    (1)求b的值；

    (2)当a＝1时，是否存在n>m>0，使得函数y＝f(x)在区间[m，n]上的函数值组成的集合也是[m，n]，若存在，求出m，n的值，否则，说明理由.

    (3)若在函数定义域内总存在区间[m，n](m<n)，使得y＝f(x)在区间[m，n]上的函数值组成的集合也是[m，n]，求实数a的取值范围.

    查看答案和解析>>

    同步练习册答案