
已知动点 到点
到点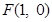 的距离,等于它到直线
的距离,等于它到直线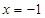 的距离.
的距离.
(Ⅰ)求点 的轨迹
的轨迹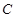 的方程;
的方程;
(Ⅱ)过点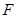 任意作互相垂直的两条直线
任意作互相垂直的两条直线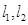 ,分别交曲线
,分别交曲线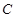 于点
于点 和
和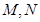 .设线段
.设线段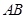 ,
,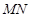 的中点分别为
的中点分别为 ,求证:直线
,求证:直线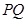 恒过一个定点;
恒过一个定点;
(Ⅲ)在(Ⅱ)的条件下,求 面积的最小值.
面积的最小值.
(Ⅰ)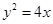 (Ⅱ)见解析(Ⅲ)
(Ⅱ)见解析(Ⅲ)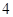
【解析】题考查圆锥曲线和直线的位置关系和综合应用,具有一定的难度,解题时要认真审题,注意挖掘隐含条件,仔细解答.
(Ⅰ)设动点M的坐标为(x,y),由题意得
|
(x-1)2+y2 |
=|x+1|,由此能求出点M的轨迹C的方程.
(Ⅱ)设A,B两点坐标分别为(x1,y1),(x2,y2),则点P的坐标由题意可设直线l1的方程为y=k(x-1)(k≠0),由
|
得k2x2-(2k2+4)x+k2=0.再由根的判别式和根与系数的关系进行求解.
(Ⅲ)题题设能求出|EF|=2,所以△FPQ面积S由均值不等式得到。
解:(Ⅰ)设动点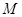 的坐标为
的坐标为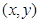 ,由题意得,
,由题意得,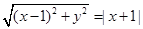 ,化简得
,化简得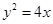 ,所以点
,所以点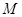 的轨迹
的轨迹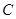 的方程为
的方程为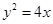 (或由抛物线定义 解) ……4分
(或由抛物线定义 解) ……4分
(Ⅱ)设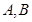 两点坐标分别为
两点坐标分别为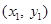 ,
,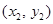 ,则点
,则点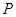 的坐标为
的坐标为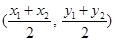 .由题意可设直线
.由题意可设直线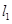 的方程为
的方程为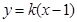
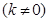 ,
,
由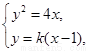 得
得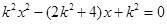 .
.
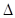
 .
.
因为直线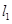 与曲线
与曲线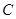 于
于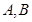 两点,所以
两点,所以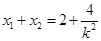 ,
,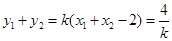 .所以点
.所以点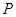 的坐标为
的坐标为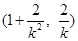 .
.
由题知,直线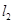 的斜率为
的斜率为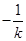 ,同理可得点
,同理可得点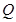 的坐标为
的坐标为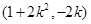 .
.
当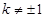 时,有
时,有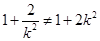 ,此时直线
,此时直线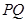 的斜率
的斜率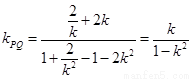 .
.
所以,直线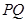 的方程为
的方程为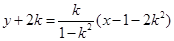 ,
,
整理得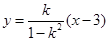 .于是,直线
.于是,直线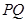 恒过定点
恒过定点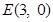 ;
;
当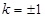 时,直线
时,直线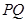 的方程为
的方程为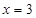 ,也过点
,也过点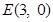 .
.
综上所述,直线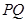 恒过定点
恒过定点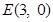 . …………10分
. …………10分
(Ⅲ)
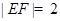 ,
,
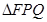 面积
面积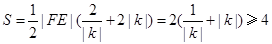 .
.
当且仅当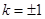 时,“
时,“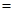 ”成立,所以
”成立,所以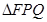 面积的最小值为
面积的最小值为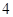 .……13分
.……13分


科目:高中数学 来源: 题型:
(14分)已知动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() 。
。
(I)求动点![]() 的轨迹C的方程;
的轨迹C的方程;
(Ⅱ)若过点![]() 的直线与曲线
的直线与曲线![]() 在
在![]() 轴左侧交于不同的两点
轴左侧交于不同的两点![]() ,点
,点![]() 满足
满足
![]() ,求直线
,求直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源: 题型:
已知动点![]() 到点
到点![]() 的距离与到直线
的距离与到直线![]() 的距离之比为
的距离之比为![]() 。
。
(I)求动点![]() 的轨迹C的方程;(Ⅱ)若过点
的轨迹C的方程;(Ⅱ)若过点![]() 的直线与曲线
的直线与曲线![]() 在
在![]() 轴左侧交于不同的两点
轴左侧交于不同的两点![]() ,点
,点![]() 满足
满足 ![]() ,求直线
,求直线![]() 在
在![]() 轴上的截距
轴上的截距![]() 的取值范围。
的取值范围。
查看答案和解析>>
科目:高中数学 来源:2012-2013学年广东省高三5月高考模拟考试理科数学试卷(解析版) 题型:解答题
已知动点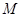 到点
到点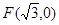 的距离与到直线
的距离与到直线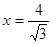 的距离之比为定值
的距离之比为定值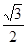 ,记
,记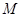 的轨迹为
的轨迹为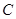 .
.

(1)求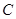 的方程,并画出
的方程,并画出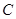 的简图;
的简图;
(2)点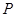 是圆
是圆 上第一象限内的任意一点,过
上第一象限内的任意一点,过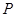 作圆的切线交轨迹
作圆的切线交轨迹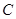 于
于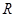 ,
,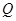 两点.
两点.
(i)证明: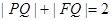 ;
;
(ii)求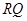 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源:2010-2011学年重庆市高三高考前冲刺试卷文数 题型:解答题
(本小题满分12分)
已知动点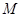 到点
到点
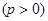 的距离比它到
的距离比它到 轴的距离多
轴的距离多 ·
·
(Ⅰ)求动点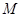 的轨迹方程;
的轨迹方程;
(Ⅱ)设动点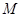 的轨迹为
的轨迹为 ,过点
,过点 的直线
的直线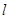 与曲线
与曲线 交于
交于 两点,若
两点,若 轴正半轴上存在点
轴正半轴上存在点 使得
使得 是以
是以 为直角顶点的等腰直角三角形,求直线
为直角顶点的等腰直角三角形,求直线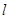 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com