
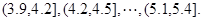 ,经过数据处理,得到如下频率分布表
,经过数据处理,得到如下频率分布表| 分组 | 频数 | 频率 |
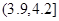 | 3 | 0.06 |
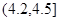 | 6 | 0.12 |
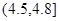 | 25 | 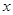 |
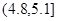 | 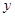 | 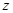 |
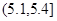 | 2 | 0.04 |
| 合计 | 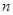 | 1.00 |
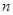 ,
,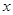 ,
,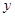 ,
,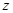 的值
的值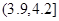 和
和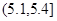 的所有同学中随机抽取两人,求两人视力差的绝对值低于
的所有同学中随机抽取两人,求两人视力差的绝对值低于 的概率
的概率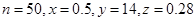 ;(Ⅱ)两人的视力差的绝对值低于
;(Ⅱ)两人的视力差的绝对值低于 的概率为
的概率为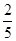 .
.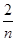 =0.04,解可得n的值,进而由x=
=0.04,解可得n的值,进而由x=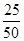 =0.5,可得x的值,由频数之和为50,可得y的值,由频率、频数的关系可得z的值;
=0.5,可得x的值,由频数之和为50,可得y的值,由频率、频数的关系可得z的值;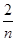 =0.04,得n=50 (2分)
=0.04,得n=50 (2分)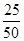 =0.5, y=50-3-6-25-2=14,z=
=0.5, y=50-3-6-25-2=14,z=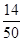 =0.28 (4分)
=0.28 (4分)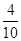 =
=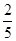 .故两人的视力差的绝对值低于0.5的概率为
.故两人的视力差的绝对值低于0.5的概率为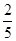 . (12分)
. (12分)

 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源:不详 题型:解答题
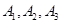 通晓日语,
通晓日语, 通晓俄语,
通晓俄语,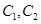 通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.
通晓韩语,从中选出通晓日语、俄语和韩语的志愿者各1名,组成一个小组.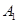 被选中的概率;(5分);(2)求
被选中的概率;(5分);(2)求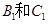 不全被选中的概率.(5分)
不全被选中的概率.(5分)查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
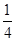 ,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=
,得到B公司面试的概率为p,且两个公司是否让其面试是独立的,记X为小王得到面试的公司个数.若X=0时的概率P(X=0)=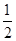 ,则随机变量X的数学期望为________.
,则随机变量X的数学期望为________.查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
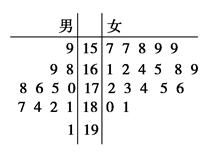
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
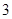 位教师安排在周一至周五中的
位教师安排在周一至周五中的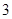 天值班,要求每人值班1天且每天至多安排1人,则恰好甲安排在另外两位教师前面值班的概率是( )
天值班,要求每人值班1天且每天至多安排1人,则恰好甲安排在另外两位教师前面值班的概率是( )A.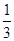 | B.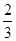 | C.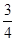 | D.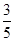 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:单选题
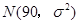 ,其中
,其中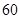 分以下的考生人数占
分以下的考生人数占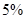 ,则数学成绩在
,则数学成绩在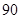 至
至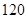 分之间的考生人数所占百分比约为 ( )
分之间的考生人数所占百分比约为 ( )A.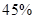 | B.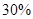 | C.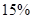 | D.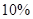 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com