
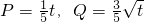 ,今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投入x万元,①当x=2时,总利润y等于多少?②试建立总利润y万元关于x的函数表达式.③如何分配投资比例,才能使总利润最大,最大利润是多少?
,今将3万元资金投入经营甲、乙两种商品,其中对甲种商品投入x万元,①当x=2时,总利润y等于多少?②试建立总利润y万元关于x的函数表达式.③如何分配投资比例,才能使总利润最大,最大利润是多少?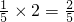 ,Q=
,Q=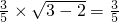 ,
,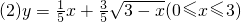
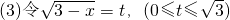

 即
即 时
时
 万元乙投入
万元乙投入 万元时收益最大,最大值为
万元时收益最大,最大值为 万元
万元

 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案 名校联盟冲刺卷系列答案
名校联盟冲刺卷系列答案 名校提分一卷通系列答案
名校提分一卷通系列答案 课程达标测试卷闯关100分系列答案
课程达标测试卷闯关100分系列答案科目:高中数学 来源: 题型:
| x |
| 5 |
| 3 |
| 5 |
| x |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x+1 |
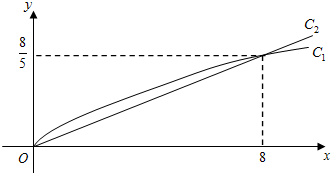
查看答案和解析>>
科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
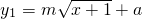 ,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.
,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.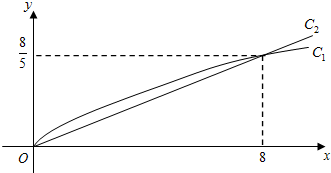
查看答案和解析>>
科目:高中数学 来源:2012-2013学年江苏省泰州市高一(上)期末数学试卷(解析版) 题型:解答题
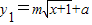 ,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.
,y2=bx,(其中m,a,b都为常数),函数y1,y2对应的曲线C1、C2如图所示.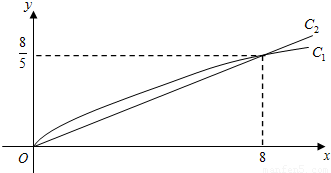
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com