
直三棱柱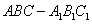 中,
中,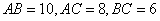 ,
,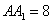 ,点D在线段AB上.
,点D在线段AB上.
(Ⅰ)若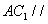 平面
平面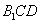 ,确定D点的位置并证明;
,确定D点的位置并证明;
(Ⅱ)当 时,求二面角
时,求二面角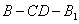 的余弦值.
的余弦值.
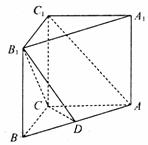
(Ⅰ)证明:当D是AB中点时,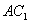 ∥平面
∥平面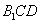 .
.
连接BC1,交B1C于E,连接DE.
因为三棱柱ABC-A1B1C1是直三棱柱,
所以侧面BB1C1C为矩形,DE为△ABC1的中位线,
所以 DE// AC1.
因为 DE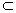 平面B1CD, AC1
平面B1CD, AC1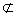 平面B1CD,
平面B1CD,
所以 AC1∥平面B1CD.
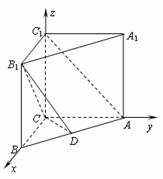
(Ⅱ)由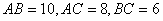 ,得AC⊥BC,以C为原点建立如图所示的空间直角坐标系C-xyz.则B(6, 0, 0),A (0, 8, 0),A1(0, 8,8),B1(6, 0, 8).设D(a, b, 0)(
,得AC⊥BC,以C为原点建立如图所示的空间直角坐标系C-xyz.则B(6, 0, 0),A (0, 8, 0),A1(0, 8,8),B1(6, 0, 8).设D(a, b, 0)( ,
, ),
),
因为 点D在线段AB上,且 , 即
, 即 .
.
所以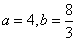 .
.
所以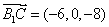 ,
,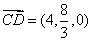 .
.
平面BCD的法向量为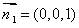 .
.
设平面B1CD的法向量为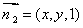 ,
,
由 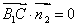 ,
,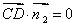 , 得
, 得 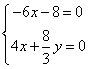 ,
,
所以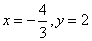 ,
,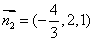 .
.
设二面角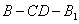 的大小为
的大小为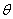 ,
,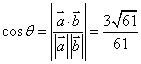 .
.
所以二面角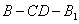 的余弦值为
的余弦值为 .
.


 中考利剑中考试卷汇编系列答案
中考利剑中考试卷汇编系列答案 教育世家状元卷系列答案
教育世家状元卷系列答案 黄冈课堂作业本系列答案
黄冈课堂作业本系列答案 单元加期末复习先锋大考卷系列答案
单元加期末复习先锋大考卷系列答案科目:高中数学 来源: 题型:
某餐厅的原料费支出 与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为
与销售额y(单位:万元)之间有如下数据,根据表中提供的全部数据,用最小二乘法得出y与x的线性回归方程为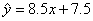 ,则表中的m的值为
,则表中的m的值为
|
| 2 | 4 | 5 | 6 | 8 |
|
| 25 | 35 |
| 55 | 75 |
A.50 B.55 C.60 D.65
查看答案和解析>>
科目:高中数学 来源: 题型:
若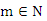 , 如题“m>0,则方程
, 如题“m>0,则方程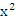
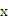
 有实根的逆否命题是
有实根的逆否命题是
若方程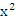
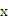
 有实根,则
有实根,则
若方程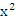
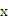
 有实根,则
有实根,则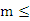
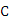 若方程
若方程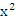
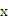
 没有实根,则
没有实根,则
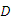 若方程
若方程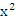
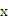
 没有实根,则
没有实根,则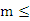
查看答案和解析>>
科目:高中数学 来源: 题型:
已知集合A={-2,-1,0,2},B={x|(X-1)(x+2)<0},则A∩B=
(A){--1,0} (B){0,1} (C){-1,0,1} (D){,0,,1,2}
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com