
设P1,P2,P3,…,Pn,…是曲线y=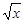 上的点列,Q1,Q2,Q3, …,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3, …,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=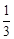 n(n+1).(13分)
n(n+1).(13分)

证明:(1)当n=1时,点P1是直线y=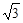 x与曲线y=
x与曲线y=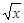 的交点,
的交点,
∴可求出P1(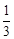 ,
,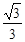 ).
).
∴a1=|OP1|=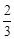 .而
.而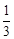 ×1×2=
×1×2=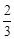 ,命题成立.(6分)
,命题成立.(6分)
(2)假设n=k(k∈N*)时命题成立,即a1+a2+…+ak=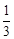 k(k+1),则点Qk的坐标为(
k(k+1),则点Qk的坐标为(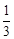 k(k+1),0),
k(k+1),0),
∴直线QkPk+1的方程为y=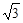 [x-
[x-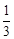 k(k+1)].代入y=
k(k+1)].代入y=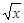 ,解得Pk+1点的坐标为
,解得Pk+1点的坐标为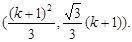
∴ak+1=|QkPk+1|=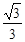 (k+1)·
(k+1)·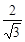 =
=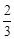 (k+1).
(k+1).
∴a1+a2+…+ak+a k+1=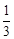 k(k+1)+
k(k+1)+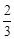 (k+1)=
(k+1)=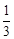 (k+1)(k+2).
(k+1)(k+2).
∴当n=k+1时,命题成立.
由(1)(2)可知,命题对所有正整数都成立.(13分)
【解析】略


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
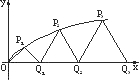 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=| x |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| x |

查看答案和解析>>
科目:高中数学 来源:2009-2010学年重庆市南开中学高三(上)数学测试卷(理科)(解析版) 题型:解答题
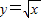 上的点列,Q1,Q2,Q3,…Qn是x轴的正半轴上的点列,O为坐标原点,且△OQ1P1,△Q1Q2P2,…,△QnQn+1Pn+1是等边三角形,设它们的边长分别为a1,a2,a3,…an,求{an}前n项和Sn.
上的点列,Q1,Q2,Q3,…Qn是x轴的正半轴上的点列,O为坐标原点,且△OQ1P1,△Q1Q2P2,…,△QnQn+1Pn+1是等边三角形,设它们的边长分别为a1,a2,a3,…an,求{an}前n项和Sn.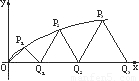
查看答案和解析>>
科目:高中数学 来源:2006年高考第一轮复习数学:13.1 数学归纳法(解析版) 题型:解答题
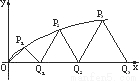 如图,设P1,P2,P3,…,Pn,…是曲线y=
如图,设P1,P2,P3,…,Pn,…是曲线y=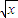 上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an=
上的点列,Q1,Q2,Q3,…,Qn,…是x轴正半轴上的点列,且△OQ1P1,△Q1Q2P2,…,△Qn-1QnPn,…都是正三角形,设它们的边长为a1,a2,…,an,…,求证:a1+a2+…+an= n(n+1).
n(n+1).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com