
若关于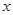 的方程
的方程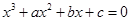 的三个根可分别作为一个椭圆、双曲线、抛物线的离心率,则
的三个根可分别作为一个椭圆、双曲线、抛物线的离心率,则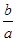 的取值范围为 .
的取值范围为 .
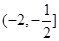
【解析】
试题分析:令f(x)=x3+ax2+bx+c
∵抛物线的离心率为1,∴1是方程f(x)=x3+ax2+bx+c=0的一个实根
∴a+b+c=-1
∴c=-1-a-b代入f(x)=x3+ax2+bx+c,
可得f(x)=x3+ax2+bx-1-a-b=(x-1)(x2+x+1)+a(x+1)(x-1)+b(x-1)=(x-1)[x2+(a+1)x+1+a+b]
设g(x)=x2+(a+1)x+1+a+b,则g(x)=0的两根满足0<x1<1,x2>1
∴g(0)=1+a+b>0,g(1)=3+2a+b<0
作出可行域,如图所示
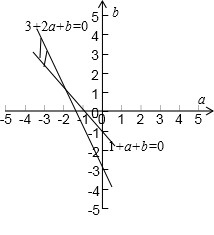
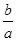 的几何意义是区域内的点与原点连线的斜率,
的几何意义是区域内的点与原点连线的斜率,
∴-2≤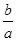 <-
<-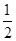 故答案为:-2≤
故答案为:-2≤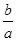 <-
<-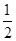
考点:本题主要考查了圆锥曲线的综合知识
点评:解题的关键是根据条件来写出不等式组,然后结合规划知识来得到。涉及到了函数的根的分布,多项式恒等等知识.属中档题。


 千里马走向假期期末仿真试卷寒假系列答案
千里马走向假期期末仿真试卷寒假系列答案科目:高中数学 来源:2011-2012学年湖南省郴州市高三下学期第六次月考理科数学 题型:填空题
设函数 ,其中
,其中 表示不超过
表示不超过 的最大整数,如:
的最大整数,如:

 . 则(i)
. 则(i) ;
;
(ii)若关于 的方程
的方程 有三个不同的根,则实数
有三个不同的根,则实数 的取值范围是.
的取值范围是.
查看答案和解析>>
科目:高中数学 来源:2011年陕西省高二数学选修1-1第三单元检测试题 题型:解答题
已知函数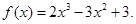
(1)求曲线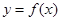 在点
在点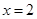 处的切线方程;
处的切线方程;
(2)若关于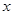 的方程
的方程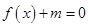 有三个不同的实根,求实数
有三个不同的实根,求实数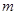 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com