
【题目】下列说法中正确的是( )
A.奇函数f(x)的图象经过(0,0)点
B.y=|x+1|+|x﹣1|(x∈(﹣4,4])是偶函数
C.幂函数y=x ![]() 过(1,1)点
过(1,1)点
D.y=sin2x(x∈[0,5π])是以π为周期的函数
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() =1(a>b>0)的上顶点为(0,2),且离心率为
=1(a>b>0)的上顶点为(0,2),且离心率为 ![]() . (Ⅰ)求椭圆C的方程;
. (Ⅰ)求椭圆C的方程;
(Ⅱ)从椭圆C上一点M向圆x2+y2=1上引两条切线,切点分别为A、B,当直线AB分别与x轴、y轴交于P、Q两点时,求|PQ|的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=logax(a>0且a≠1)在区间[1,2]上的最大值与函数g(x)=﹣ ![]() 在区间[1,2]上的最大值互为相反数.
在区间[1,2]上的最大值互为相反数.
(1)求a的值;
(2)若函数F(x)=f(x2﹣mx﹣m)在区间(﹣∞,1﹣ ![]() )上是减函数,求实数m的取值范围.
)上是减函数,求实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)= ![]() ﹣
﹣ ![]() ,若规定<x>表示不小于x的最小整数,则函数y=<f(x)>的值域是( )
,若规定<x>表示不小于x的最小整数,则函数y=<f(x)>的值域是( )
A.{0,1}
B.{0,﹣1}
C.{﹣1,1}
D.{﹣1,0,1}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知正方体ABCD﹣A1B1C1D1的棱长为1,给出下列四个命题: ①对角线AC1被平面A1BD和平面B1 CD1三等分;
②正方体的内切球、与各条棱相切的球、外接球的表面积之比为1:2:3;
③以正方体的顶点为顶点的四面体的体积都是 ![]() ;
;
④正方体与以A为球心,1为半径的球在该正方体内部部分的体积之比为6:π
其中正确命题的序号为 . 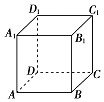
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设实数a∈R,函数 ![]() 是R上的奇函数. (Ⅰ)求实数a的值;
是R上的奇函数. (Ⅰ)求实数a的值;
(Ⅱ)当x∈(1,1)时,求满足不等式f(1m)+f(1m2)<0的实数m的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】甲、乙、丙、丁四个物体同时从某一点出发向同一个方向运动,其路程fi(x)(i=1,2,3,4)关于时间x(x≥0)的函数关系式分别为 ![]() ,
, ![]() ,f3(x)=x,f4(x)=log2(x+1),有以下结论: ①当x>1时,甲走在最前面;
,f3(x)=x,f4(x)=log2(x+1),有以下结论: ①当x>1时,甲走在最前面;
②当x>1时,乙走在最前面;
③当0<x<1时,丁走在最前面,当x>1时,丁走在最后面;
④丙不可能走在最前面,也不可能走在最后面;
⑤如果它们一直运动下去,最终走在最前面的是甲.
其中,正确结论的序号为(把正确结论的序号都填上,多填或少填均不得分).
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com