
(本小题满分12分)
某高校设计了一个实验学科的实验考查方案:考生从6道备选题中一次性随机抽取3题,按照题目要求独立完成全部实验操作。规定:至少正确完成其中2题的便可提交通过。已知6道备选题中考生甲有4道题能正确完成,2道题不能完成;考生乙每题正确完成的概率都是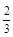 ,且每题正确完成与否互不影响。
,且每题正确完成与否互不影响。
(Ⅰ)分别写出甲、乙两考生正确完成题数的概率分布列,并计算数学期望;
(Ⅱ)试从两位考生正确完成题数的数学期望及至少正确完成2题的概率分析比较两位考生的实验操作能力.
(1)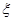
1 2 3 P 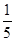
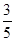
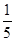

(2) 可以判断甲的实验操作能力较强。
解析试题分析:解:(Ⅰ)设考生甲、乙正确完成实验操作的题数分别为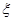 ,
,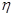 ,则
,则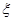 的取值分别为1、2、3,
的取值分别为1、2、3,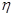 的取值分别,0、1、2、3,
的取值分别,0、1、2、3,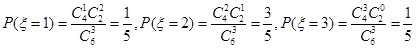
所以考生甲正确完成实验操作的题数的概率分布列为: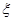
1 2 3 P 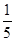
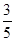
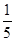
 ………………5分
………………5分
因为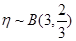 ,所以考生乙正确完成实验操作的题数的概率分布列为:
,所以考生乙正确完成实验操作的题数的概率分布列为: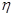
0 1 2 3 P 
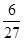
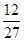
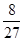
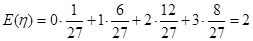 ………………8分
………………8分
(Ⅱ)因为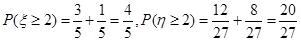
所以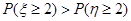 ………………10分
………………10分
从做对题的数学期望考察,两人水平相当;从至少正确完成2题的概率考察,甲通过的可能性大,因此可以判断甲的实验操作能力较强。 ………………10分
考点:分布列的求解
点评:解决该试题的关键是利用等可能事件是概率公式得到概率值,进而求解,属于基础题。


科目:高中数学 来源: 题型:解答题
现有长分别为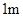 、
、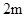 、
、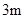 的钢管各
的钢管各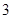 根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取
根(每根钢管质地均匀、粗细相同且附有不同的编号),从中随机抽取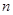 根(假设各钢管被抽取的可能性是均等的,
根(假设各钢管被抽取的可能性是均等的, ),再将抽取的钢管相接焊成笔直的一根.
),再将抽取的钢管相接焊成笔直的一根.
(1)当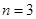 时,记事件
时,记事件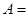 {抽取的
{抽取的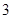 根钢管中恰有
根钢管中恰有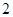 根长度相等},求
根长度相等},求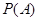 ;
;
(2)当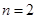 时,若用
时,若用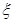 表示新焊成的钢管的长度(焊接误差不计),①求
表示新焊成的钢管的长度(焊接误差不计),①求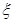 的分布列;
的分布列;
②令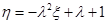 ,
,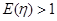 ,求实数
,求实数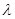 的取值范围.
的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
甲设计了一个摸奖游戏,在一个口袋中装有同样大小的10个球,分别标有数字0,1,2,……9这十个数字,摸奖者交5元钱可参加一回摸球活动,一回摸球活动的规则是:摸奖者在摸球前先随机确定(预报)3个数字,然后开始在袋中不放回地摸3次球,每次摸一个,摸得3个球的数字与预先所报数字均不相同的奖1元,有1个数字相同的奖2元,2个数字相同的奖10元,3个数字相同的奖50元,设ξ为摸奖者一回所得奖金数,求ξ的分布列和摸奖人获利的数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题13分)已知关于x的一元二次函数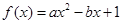 ,分别从集合P和Q中随机取一个数a和b得到数列
,分别从集合P和Q中随机取一个数a和b得到数列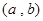 。
。
(1)若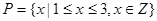 ,
,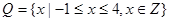 ,列举出所有的数对
,列举出所有的数对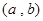 ,并求函数
,并求函数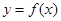 有零点的概率;
有零点的概率;
(2)若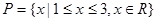 ,
,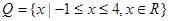 ,求函数
,求函数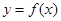 在区间
在区间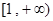 上是增函数的概率。
上是增函数的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本题满分12分)因金融危机,某公司的出口额下降,为此有关专家提出两种促进出口的方案,每种方案都需要分两年实施.若实施方案一,预计第一年可以使出口额恢复到危机前的1.0倍、0.9倍、0.8倍的概率分别为0.3、0.3、0.4;第二年可以使出口额为第一年的1.25倍、1.0倍的概率分别是0.5、0.5.若实施方案二,预计第一年可以使出口额恢复到危机前的1.2倍、l.0倍、0.8倍的概率分别为0.2、0.3、0.5;第二年可以使出口额为第一年的1.2倍、1.0倍的概率分别是0.4、0.6.实施每种方案第一年与第二年相互独立.令ζ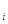 (
(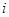 =1,2)表示方案
=1,2)表示方案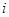 实施两年后出口额达到危机前的倍数。
实施两年后出口额达到危机前的倍数。
(Ⅰ)写出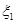 、
、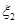 的分布列;
的分布列;
(Ⅱ)实施哪种方案,两年后出口额超过危机前出口额的概率更大?
(Ⅲ)不管哪种方案,如果实施两年后出口额达不到、恰好达到、超过危机前出口额,预计利润分别为10万元、15万元、20万元,问实施哪种方案的平均利润更大。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分12分)
有编号为l,2,3,…, 的
的 个学生,入坐编号为1,2,3,…,
个学生,入坐编号为1,2,3,…, 的
的 个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为
个座位.每个学生规定坐一个座位,设学生所坐的座位号与该生的编号不同的学生人数为 ,已知
,已知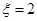 时,共有6种坐法.
时,共有6种坐法.
(1)求 的值;
的值;
(2)求随机变量 的概率分布列和数学期望.
的概率分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
(本小题满分13分)
设a、b、c分别是先后掷一枚质地均匀的正方体骰子三次得到的点数.
(1)求使函数 在R上不存在极值点的概率;
在R上不存在极值点的概率;
(2)设随机变量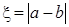 ,求
,求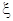 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个盒子中有5只同型号的灯泡,其中有3只合格品,2只不合格品。现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(1)求第一次取到不合格品,且第二次取到的是合格品的概率;
(2)求至少有一次取到不合格品的概率。
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
一个均匀的正四面体的四个面上分别涂有1,2,3,4四个数字,现随机投掷两次,正四面体面朝下的数字分别为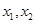 ,记
,记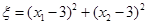 .
.
(1)分别求出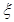 取得最大值和最小值时的概率; (2)求
取得最大值和最小值时的概率; (2)求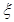 的分布列及数学期望.
的分布列及数学期望.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com