将7×7的棋盘中的2个方格染成黄色.其余的染成绿色．若一种染色法经过在棋盘的平面中旋转而得到.那么这两种染色法看着是同一种.则有种不同的染色法．题目和参考答案——青夏教育精英家教网—

精英家教网 > 高中数学 > 题目详情

将7×7的棋盘中的2个方格染成黄色，其余的染成绿色．若一种染色法经过在棋盘的平面中旋转而得到，那么这两种染色法看着是同一种，则有种不同的染色法．

【答案】分析：根据是7×7棋盘，有4条对称轴，不同染色法有

种，还有对称轴上关于中心对称的情况

种，把这两个数相加，即得所求．
解答：解：因为是7×7棋盘，有4条对称轴，不同染色法有

=294种，
还有对称轴上关于中心对称的情况 12÷2=6 种，
故一共有294+6=300种，
故答案为 300．
点评：本题主要考查排列、组合以及两个基本原理的应用，要特别注意重复的情况，属于中档题．

练习册系列答案

年级	高中课程	年级	初中课程
高一	高一免费课程推荐！	初一	初一免费课程推荐！
高二	高二免费课程推荐！	初二	初二免费课程推荐！
高三	高三免费课程推荐！	初三	初三免费课程推荐！
更多初中、高中辅导课程推荐,点击进入>>

相关习题

科目：高中数学 来源：2012-2013学年黑龙江省鹤岗一中高二（上）期末数学试卷（理科）（解析版） 题型：解答题

为了研究化肥对小麦产量的影响，某科学家将一片土地划分成200个50m²的小块，并在100个小块上施用新化肥，留下100个条件大体相当的小块不施用新化肥．下表1和表2分别是施用新化肥和不施用新化肥的小麦产量频数分布表（小麦产量单位：kg）
表1：施用新化肥小麦产量频数分布表

小麦产量	[0，10）	[10，20）	[20，30）	[30，40）	[40，50）
频数	10	35	40	10	5

表2：不施用新化肥小麦产量频数分布表

小麦产量	[0，10）	[10，20）	[20，30）	[30，40）
频数	15	50	30	5

（1）完成下面频率分布直方图；

施用新化肥后小麦产量的频率分布直方图不施用新化肥后小麦产量的频率分布直方图
（2）统计方法中，同一组数据常用该组区间的中点值作为代表，据此估计施用化肥和不施用化肥的一小块土地的小麦平均产量；
（3）完成下面2×2列联表，并回答能否有99.5%的把握认为“施用新化肥和不施用新化肥的小麦产量有差异”
表3：

	小麦产量小于20kg	小麦产量不小于20kg	合计
施用新化肥	a=	b=
不施用新化肥	c=	d=
合计			n=

附：

P（K²≥k）	0.050 0.010 0.005 0.001
k	3.841 6.635 7.879 10.828

查看答案和解析>>

科目：高中数学 来源：2009-2010学年广东省中山市高二（上）期末数学试卷（理科）（解析版） 题型：选择题

我市某企业在2009年元月份为战胜国际背景下的金融危机，积极响应国务院提出的产业振兴计划，对每周的自动化生产项目中进行程序优化．在程序设计中，需要采用一个七进制计数器，所谓七进制即“逢七进一”，如1203_（7）表示七进制数，将它转换成十进制形式，是1×7³+2×7²+0×7¹+3×7=444，那么将七进制数

_（7）转换成十进制形式是（）
A．7¹³-7
B．7¹²-7
C．7¹²-1
D．7¹¹-1

查看答案和解析>>

科目：高中数学 来源：2009-2010学年广东省中山市高二（上）期末数学试卷（文科）（解析版） 题型：选择题

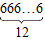_（7）转换成十进制形式是（）
A．7¹³-7
B．7¹²-7
C．7¹²-1
D．7¹¹-1

查看答案和解析>>

科目：高中数学 来源：2011年江西省抚州市临川二中高考数学一模试卷（文科）（解析版） 题型：解答题

某中学研究性学习小组，为了考察高中学生的作文水平与爱看课外书的关系，在本校高三年级随机调查了50名学生．调査结果表明：在爱看课外书的25人中有18人作文水平好，另7人作文水平一般；在不爱看课外书的25人中有6人作文水平好，另19人作文水平一般．
（Ⅰ）试根据以上数据建立一个2×2列联表，并运用独立性检验思想，指出有多大把握认为中学生的作文水平与爱看课外书有关系？
（Ⅱ）将其中某5名爱看课外书且作文水平好的学生分别编号为1，2，3，4，5，某5名爱看课外书且作文水平一般的学生也分别编号为1，2，3，4，5，从这两组学生中各任选1人进行学习交流，求被选取的两名学生的编号之和为3的倍数或4的倍数的概率．
附：

临界值表：

P（K²≥k）	0.10	0.05	0.025	0.010	0.005	0.001
k	2.706	3.841	5.024	6.635	7.879	10.828

查看答案和解析>>

同步练习册答案

练习册

高中

初中

小学