
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
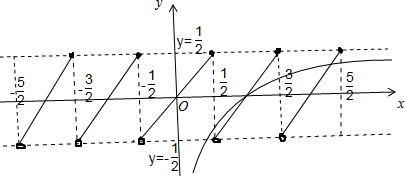 解:①x∈(0,1)时,m=
解:①x∈(0,1)时,m=| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |


科目:高中数学 来源:2012-2013学年北京市海淀区八一中学高三(上)周练数学试卷(2)(理科)(解析版) 题型:选择题
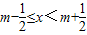 (其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题:
(其中m为整数),则m叫离实数x最近的整数,记作[x]=m,已知f(x)=|[x]-x|,下列四个命题: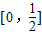 ; ②函数f(x)是R上的增函数;
; ②函数f(x)是R上的增函数;查看答案和解析>>
科目:高中数学 来源:2014届江苏省高二下学期期中考试文科数学试卷(解析版) 题型:填空题
给出定义:若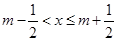 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m,在此基础上给出关于函数
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m,在此基础上给出关于函数 的四个命题:
的四个命题:
①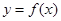 的定义域是R,值域为
的定义域是R,值域为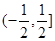 ;
;
②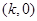 是
是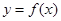 图像的对称中心,其中
图像的对称中心,其中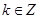 ;
;
③函数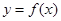 的最小正周期是1;
的最小正周期是1;
④函数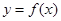 在
在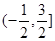 上是增函数.
上是增函数.
其中真命题的序号是______.
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广西省高三年级第四次月考理科数学试卷 题型:填空题
给出定义:若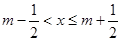 (其中m为整数),则m叫做离实数x最近的整数,记作
(其中m为整数),则m叫做离实数x最近的整数,记作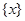 ,即
,即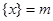 ,在此基础上给出下列关于函数
,在此基础上给出下列关于函数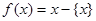 的四个命题:
的四个命题:
①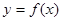 的定义域是R,值域是
的定义域是R,值域是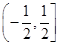 ;②点
;②点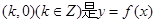 的图像的对称中心;③函数
的图像的对称中心;③函数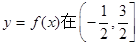 上是增函数; ④函数
上是增函数; ④函数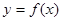 的最小正周期为1;
的最小正周期为1;
则其中真命题是
查看答案和解析>>
科目:高中数学 来源:2010-2011学年河南省毕业班高三高考适应性考试数学理卷 题型:选择题
给出定义:若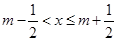 (其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数
(其中m为整数),则m叫做离实数x最近的整数,记作{x},即{x}=m在此基础上给出下列关于函数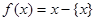 的四个命题:
的四个命题:
①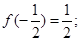 ②
②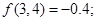
③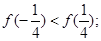 ④
④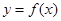 的定义域为R,值域是
的定义域为R,值域是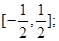
则其中真命题的序号是 ( )
A.①② B.①③ C.②④ D.③④
第Ⅱ卷
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com