
 设
设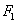 ,
,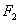 分别为椭圆
分别为椭圆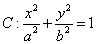
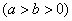 的左、右焦点,过
的左、右焦点,过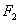 的直线
的直线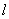 与椭圆
与椭圆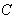 相交于
相交于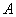 ,
,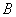 两点,直线
两点,直线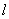 的倾斜角为
的倾斜角为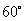 ,
,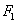 到直线
到直线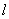 的距离为
的距离为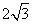 .
.
(Ⅰ)求椭圆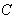 的焦距;
的焦距;
(Ⅱ)如果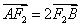 ,求椭圆
,求椭圆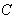 的方程.
的方程.
解:(Ⅰ) f(x)的定义域为(0,+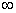 ),
),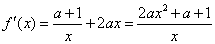 .
.
当a≥0时,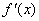 >0,故f(x)在(0,+
>0,故f(x)在(0,+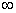 )单调增加;
)单调增加;
当a≤-1时,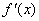 <0, 故f(x)在(0,+
<0, 故f(x)在(0,+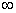 )单调减少;
)单调减少;
当-1<a<0时,令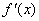 =0,解得x=
=0,解得x= .当x∈(0,
.当x∈(0,  )时,
)时, 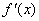 >0;
>0;
x∈( ,+
,+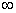 )时,
)时,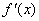 <0, 故f(x)在(0,
<0, 故f(x)在(0,  )单调增加,在(
)单调增加,在( ,+
,+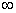 )单调减少.
)单调减少.
(Ⅱ)不妨假设x1≥x2.由于a≤-2,故f(x)在(0,+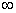 )单调减少.
)单调减少.
所以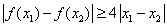 等价于
等价于
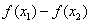 ≥4xx2,
≥4xx2,
即f(x2)+ 4x2≥f(x1)+ 4x1.
令g(x)=f(x)+4x,则
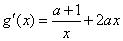 +4
+4
=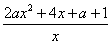 .
.
于是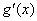 ≤
≤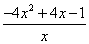 =
= ≤0.
≤0.
从而g(x)在(0,+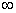 )单调减少,故g(x1) ≤g(x2),
)单调减少,故g(x1) ≤g(x2),
即 f(x1)+
4x1≤f(x2)+ 4x2,故对任意x1,x2∈(0,+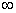 ) ,
) ,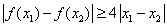 .
.
请考生在第(22)、(23)、(24)三题中任选一题做答,如果多做,则按所做的第一题记分。做答时用2B铅笔在答题卡上把所选题目对应题号下方的方框涂黑。


 轻松课堂单元期中期末专题冲刺100分系列答案
轻松课堂单元期中期末专题冲刺100分系列答案科目:高中数学 来源: 题型:
(08年新建二中三模)设![]() 、
、![]() 分别为椭圆
分别为椭圆![]() 的左、右顶点,椭圆长半轴的长等于焦距,且
的左、右顶点,椭圆长半轴的长等于焦距,且![]() 为它的右准线.
为它的右准线.
⑴求椭圆的方程;
⑵设![]() 为右准线上不同于点
为右准线上不同于点![]() 的任意一点,若直线
的任意一点,若直线![]() 、
、![]() 分别与椭圆相交于异于
分别与椭圆相交于异于![]() 、
、![]() 的点
的点![]() 、
、![]() ,证明:点
,证明:点![]() 在以
在以![]() 为直径的圆内.
为直径的圆内.

查看答案和解析>>
科目:高中数学 来源:2012-2013学年四川宜宾高三第二次模拟考试文科数学试卷(解析版) 题型:解答题
设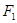 、
、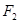 分别为椭圆
分别为椭圆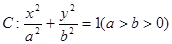 的左、右两个焦点.
的左、右两个焦点.
(Ⅰ)
若椭圆C上的点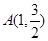 到
到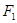 、
、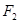 两点的距离之和等于4, 写出椭圆C的方程和离心率.;
两点的距离之和等于4, 写出椭圆C的方程和离心率.;
(Ⅱ)
若M、N是椭圆C上关于原点对称的两点,点P是椭圆上除M、N外的任意一点, 当直线PM、PN的斜率都存在, 并记为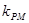 、
、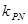 时, 求证:
时, 求证: 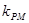 ·
·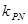 为定值.
为定值.
查看答案和解析>>
科目:高中数学 来源:2012届辽宁省营口市高二上学期期末教学质量检测理科数学 题型:解答题
设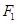 ,
,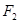 分别为椭圆
分别为椭圆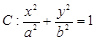
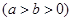 的左、右焦点,过
的左、右焦点,过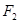 的直
的直
线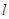 与椭圆
与椭圆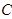 相交于
相交于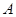 ,
,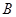 两点,直线
两点,直线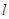 的倾斜角为
的倾斜角为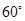 ,
, 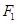 到直线
到直线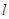 的距离为
的距离为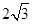 ;
;
(1)求椭圆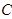 的焦距;
的焦距;
(2)如果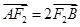 ,求椭圆
,求椭圆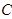 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
设![]() ,
,![]() 分别为椭圆
分别为椭圆![]()
![]() 的左、右焦点,过
的左、右焦点,过![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,直线
两点,直线![]() 的倾斜角为
的倾斜角为![]() ,
,![]() 到直线
到直线![]() 的距离为
的距离为![]() .
.
(Ⅰ)求椭圆![]() 的焦距;
的焦距;
(Ⅱ)如果![]() ,求椭圆
,求椭圆![]() 的方程.
的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com