
分析:这是一个几何概型问题,用弧长公式将角度与半径联系起来,转化为角度的几何概型问题,根据问题找出事件A的几何度量和事件Ω的几何度量.
解法一:在⊙O上有一定点A,任取一点B与A连结,则弦长超过半径的![]() 倍,即为∠AOB的度数大于90°,记“弦长超过半径的
倍,即为∠AOB的度数大于90°,记“弦长超过半径的![]() 倍”为事件C,则C表示的范围是∠AOB∈[90°,270°],
倍”为事件C,则C表示的范围是∠AOB∈[90°,270°],
由几何概型的概率公式得P(C)=![]() .
.
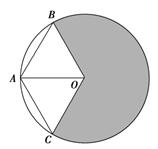
解法二:设⊙O的半径为r,在⊙O上任取一点B,连结弦AB,使得AB=![]() r,取AB的中点C,则OC⊥BC且BC=
r,取AB的中点C,则OC⊥BC且BC=![]() r,在RT△BCO中,∠BOC=45°,由圆的对称性知,⊙O上还存在一点D满足DA=
r,在RT△BCO中,∠BOC=45°,由圆的对称性知,⊙O上还存在一点D满足DA=![]() r,所以满足条件“弦长超过半径的
r,所以满足条件“弦长超过半径的![]() 倍”的⊙O上的点应该在⊙O上的
倍”的⊙O上的点应该在⊙O上的![]() 部分(不含点A的那段圆弧),而
部分(不含点A的那段圆弧),而![]() =
=![]() 圆周,所以P(“弦长超过半径的
圆周,所以P(“弦长超过半径的![]() 倍”)=
倍”)=![]() .
.


 寒假学与练系列答案
寒假学与练系列答案科目:高中数学 来源:2012人教A版高中数学必修三3.3几何概型练习题(一)(解析版) 题型:选择题
设A为圆周上一定点,在圆周上等可能地任取一点与A连接,则弦长超过半径的概率为( )
A.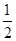 B.
B.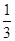
C.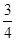 D.
D.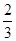
查看答案和解析>>
科目:高中数学 来源:2010-2011年山东省高一下学期期中考试数学试卷 题型:选择题
设A为圆周上一定点,在圆周上等可能地任取一点与A连结,则弦长超过半径的概率是
A.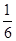 B.
B.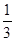 C.
C.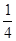 D.
D.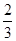
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com