
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源:2011-2012学年广东省肇庆市高三复习必修5综合练习2数学 题型:选择题
某人为了观看2008年奥运会,从2001年起,每年5月10日到银行存入a元定期储蓄,若年利率为P,且保持不变,并约定每年到期存款均自动转为新的一年定期,到2008年5月10日将所有存款和利息全部取回,则可取回的钱的总数(元)为 ( )
A. B.
B.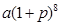 C.
C. D.
D.
查看答案和解析>>
科目:高中数学 来源:不详 题型:填空题
查看答案和解析>>
科目:高中数学 来源:2011-2012学年福建省厦门市五显中学高二(上)期中数学试卷(理科)(解析版) 题型:选择题
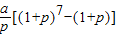

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com