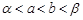试题分析:首先把方程化为一般形式,由于α,β是方程的解,根据根与系数的关系即可得到a,b,α,β之间的关系,然后对四者之间的大小关系进行讨论即可判断
方法1:方程化为一般形式得:x2-(a+b)x+ab-1=0,
∵α,β是方程(x-a)(x-b)-1=0的两根,
∴α+β=a+b
∴当α>a时,又∵a<b,α<β则:a<α<β<b;
当α>b时,β<a,又∵a<b,α<β,则不成立.
方法2:令w=(x-a)(x-b),作出图象抛物线与x轴交于点a,b.则y=(x-a)(x-b)-1的图象是将w向下平移1个单位得到,则α、β是抛物线y与x轴的两个交点.在图上可以直接看到α<a<b<β.
故答案为:α<a<b<β.,选A.
点评:解决该试题的关键是对a,b,α,β大小关系的讨论,同时也是此题的难点,讨论的原则就是根与 系数a的大小情况。

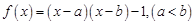 ,并且
,并且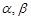 是方程
是方程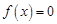 的两根
的两根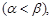 则实数
则实数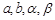 的大小关系是
的大小关系是