
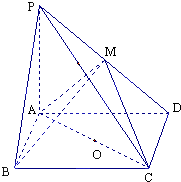
 在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M
在四棱锥P-ABCD中,底面ABCD是矩形,PA⊥平面ABCD,PA=AD=4,AB=2.以AC的中点O为球心、AC为直径的球面交PD于点M分析 (1)利用线面、面面垂直的判定定理、性质定理即可证明;
(2)通过建立空间直角坐标系,先求出平面ABM的法向量,进而即可求出线面角.
解答 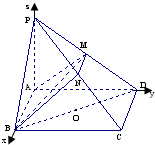 解:(1)证明:由题意,M在以BD为直径的球面上,则BM⊥PD,
解:(1)证明:由题意,M在以BD为直径的球面上,则BM⊥PD,
∵PA⊥平面ABCD,∴PA⊥AB,
又∵AB⊥AD,PA∩AD=A,
∴AB⊥平面PAD,∴AB⊥PD,
∵BM∩AB=B,
∴PD⊥平面ABM,又PD?平面PCD,
∴平面ABM⊥平面PCD.
(2)由(1)可知:PD⊥平面ABM,∴PD⊥AM,又在Rt△PAD,PA=AD,∴PM=MD.
如图所示,建立空间直角坐标系,
则A(0,0,0),P(0,0,4),B(2,0,0),C(2,4,0),D(0,4,0),M(0,2,2),
由(1)可知:$\overrightarrow{PD}$是平面ABM的一个法向量$\overrightarrow{PD}$=(0,4,-4),
又$\overrightarrow{PC}$=(2,4,-4),
设PC与平面ABM所成的角为θ,
则sinθ=|cos<$\overrightarrow{PD}$,$\overrightarrow{PC}$>|=$\frac{|\overrightarrow{PD}•\overrightarrow{PC}|}{|\overrightarrow{PD}|•|\overrightarrow{PC}|}$=$\frac{32}{\sqrt{32}•\sqrt{36}}$=$\frac{2\sqrt{2}}{3}$.
点评 熟练掌握线面、面面垂直的判定定理、性质定理及通过建立空间直角坐标系利用平面的法向量与斜向量求出线面角是解题的关键.


 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | (1) | B. | (2)(3) | C. | (1)(3) | D. | (1)(4) |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com