已知变量
与
正相关，且由观测数据算得样本平均数
，
，则由该观测的数据算得的线性回归方程可能是
A． | B． |
C． | D． |
科目：高中数学 来源： 题型：单选题
下表提供了某厂节能降耗技术改造后生产某产品过程中记录的产量
（吨）与相应的生产能耗
（吨）的几组对应数据. 根据表中提供的数据，求出关于的线性回归方程是
，那么表中
的值是（ ）
| 3 | 4 | 5 | 6 |
| 2.5 | | 4 | 4.5 |
B.
C.
D.
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
在独立性检验中，统计量
有两个临界值：3.841和6.635；当＞3.841时，有95%的把握说明两个事件有关，当＞6.635时，有99%的把握说明两个事件有关，当
3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的="20." 87，根据这一数据分析，认为打鼾与患心脏病之间
| A．有95%的把握认为两者有关 |
| B．约有95%的打鼾者患心脏病 |
| C．有99%的把握认为两者有关 |
| D．约有99%的打鼾者患心脏病 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
若对于预报变量y与解释变量x的10组统计数据的回归模型中，计算R2=0.95，又知残差平方和为120.55，那么
的值为（ ）
| A．241．1 | B．245．1 | C．2411 | D．2451 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
在独立性检验中，统计量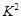
有两个临界值：3.841和6.635；当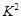＞3.841时，有95%的把握说明两个事件有关，当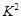＞6.635时，有99%的把握说明两个事件有关，当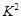
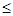3.841时，认为两个事件无关.在一项打鼾与患心脏病的调查中，共调查了2000人，经计算的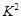=20.87，根据这一数据分析，认为打鼾与患心脏病之间 ( )
| A．有95%的把握认为两者有关 | B．约有95%的打鼾者患心脏病 |
| C．有99%的把握认为两者有关 | D．约有99%的打鼾者患心脏病 |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
某产品的广告费用x与销售额y的统计数据如下表：
| 广告费用x（万元） | 4 | 2 | 3 | 5 |
| 销售额y（万元） | 49 | 26 | 39 | 58 |
中的
，据此模型预报广告费用为
万元时销售额为（ ）．
万元 B．
万元 C．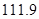
万元 D．
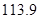万元查看答案和解析>>
科目：高中数学 来源： 题型：单选题
下列命题中的真命题是（ ）
?若命题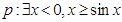
，命题
：函数
仅有两个零点，则命题
为真命题；
?若变量
的一组观测数据
均在直线
上，则
的线性相关系数
;
?若
，则使不等式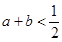
成立的概率是
．
| A．?? | B．?? | C．? | D．?? |
查看答案和解析>>
科目：高中数学 来源： 题型：单选题
计算机中常用十六进制，采用数字0～9和字母A～F共16个计数符号与十进制得对应关系如下表：
| 16进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | A | B | C | D | E | F |
| 10进制 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
，代入检验知，只有直线
过点
名学生的学习情况，采用系统抽样的方法，从中抽取容量为
的样本，则分段的间隔为（ ）
