Question

8个身高不相同的人排成前后两排，每排4人，要求后排的人都比他对应的前排的人高，则不同的排法有    种．

Answer 1

【答案】分析：由题意8个身高不相同的人排成前后两排，每排4人，要求后排的人都比他对应的前排的人高，前后2人为一组，分4次选出的组合，即可得到排法的种数．
解答：解：8个身高不相同的人排成前后两排，每排4人，要求后排的人都比他对应的前排的人高，
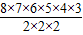
前后高度不同，自左至右的选法种数为：C₈²C₆²C₄²C₂²==2520．
故答案为：2520．
点评：本题是中档题，考查有限制条件的排列组合知识，注意本题的解答方法，简单的计数原理与组合数的应用，也可以利用平均分组处理．