
分析 (Ⅰ)由题意可得$\left\{\begin{array}{l}b=\sqrt{5}\\ e=\frac{c}{a}=\frac{2}{3}\\{a^2}={b^2}+{c^2}.\end{array}\right.$解得即可,
(Ⅱ)法一:设A(4,y),F1(-2,0),根据线段F1A的垂直平分线经过点F2得到|F1F2|=|F2A|,代值计算即可y的值,即可求出直线方程,
法二:设过点F1(-2,0)的直线l的斜率为k,则直线l的方程为y=k(x+2),再设AF1的中点P(x0,y0).根据PF2⊥F1A,即可求出k的值,
(Ⅲ)点B在椭圆C上,设B(m,n),n∈[-$\sqrt{5}$,0)∪(0,$\sqrt{5}$],A(4,y),根据两点之间的距离公式,化简整理,再根据函数的单调性求出最值.
解答 解:( I)由$\left\{\begin{array}{l}b=\sqrt{5}\\ e=\frac{c}{a}=\frac{2}{3}\\{a^2}={b^2}+{c^2}.\end{array}\right.$解得$\left\{\begin{array}{l}a=3\\ c=2.\end{array}\right.$
所以椭圆C的方程为$\frac{{x}^{2}}{9}$+$\frac{{y}^{2}}{5}$=1.
( II)法一:设A(4,y),F1(-2,0),
因为线段F1A的垂直平分线经过点F2,
所以|F1F2|=|F2A|.
由2c=4=$\sqrt{(4-2)^{2}+{y}^{2}}$,解得y=±2$\sqrt{3}$.
所以直线l的方程为y=±$\frac{\sqrt{3}}{3}$(x+2).
( II)法二
设过点F1(-2,0)的直线l的斜率为k,显然k存在.
则直线l的方程为y=k(x+2).
所以A(4,6k).
设AF1的中点P(x0,y0).
则${x_0}=\frac{-2+4}{2}=1,{y_0}=\frac{0+6k}{2}=3k$.
所以P(1,3k).
因为PF2⊥F1A,
所以$\frac{3k-0}{1-2}•k=-1$.
所以$k=±\frac{{\sqrt{3}}}{3}$.
所以直线l的方程为y=±$\frac{\sqrt{3}}{3}$(x+2).
( III)点B在椭圆C上,设B(m,n),n∈[-$\sqrt{5}$,0)∪(0,$\sqrt{5}$],A(4,y).
因为OA⊥OB,
所以$\overrightarrow{OA}•\overrightarrow{OB}=0$,即4m+ny=0.
因为点B在椭圆C上,
所以$\frac{{m}^{2}}{9}$+$\frac{{n}^{2}}{5}$=1,
所以|AB|2=(m-4)2+(n-y)2=m2-8m+16+n2-2ny+y2=m2-8m+16+n2+8m+y2,
=m2+16+n2+y2=m2+16+n2+($\frac{-4m}{n}$)2,
=9(1-$\frac{{n}^{2}}{5}$)+16+n2+$\frac{16×9(1-\frac{{n}^{2}}{5})}{{n}^{2}}$,
=$\frac{144}{{n}^{2}}$-$\frac{4{n}^{2}}{5}$-$\frac{19}{5}$
设t=n2,t∈(0,5]
设$g(t)=\frac{144}{t}-\frac{4t}{5}-\frac{19}{5}$.
因为$g'(t)=\frac{-144}{t^2}-\frac{4}{5}<0$,
所以g(t)在(0,5]上单调递减.
所以当t=5,即$n=±\sqrt{5}$时,|AB|min=$\sqrt{21}$.
点评 本题考查椭圆的方程和性质,主要考查椭圆的离心率和方程的运用,以及两点的距离公式和函数的应用,考查运算能力,属于中档题.


 高中必刷题系列答案
高中必刷题系列答案科目:高中数学 来源: 题型:解答题
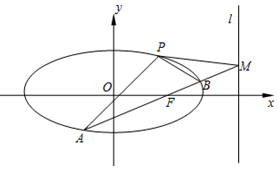 如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$P(1,\frac{3}{2})$,离心率$e=\frac{1}{2}$.
如图,已知椭圆$C:\frac{x^2}{a^2}+\frac{y^2}{b^2}=1({a>b>0})$经过点$P(1,\frac{3}{2})$,离心率$e=\frac{1}{2}$.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
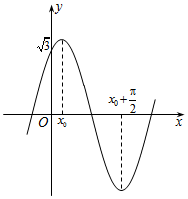 已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则函数f(x)的解析式的值为( )
已知函数$f(x)=2sin(ωx+φ)(ω>0,|φ|<\frac{π}{2})$的图象如图所示,则函数f(x)的解析式的值为( )| A. | $f(x)=2sin(2x+\frac{π}{6})$ | B. | $f(x)=2sin(2x+\frac{π}{3})$ | C. | $f(x)=2sin(x+\frac{π}{6})$ | D. | $f(x)=2sin(x+\frac{π}{3})$ |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
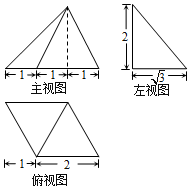
| A. | $\frac{{2\sqrt{3}}}{3}$ | B. | $\frac{{4\sqrt{3}}}{3}$ | C. | 2 | D. | $\frac{{5\sqrt{3}}}{3}$ |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com