
 时,恒有(x-a)2+(y-b)2≥2,则以a,b为坐标的点(a,b)所形成的平面区域的面积等于 .
时,恒有(x-a)2+(y-b)2≥2,则以a,b为坐标的点(a,b)所形成的平面区域的面积等于 .  ,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用求最优解的方法,结合题中条件:“恒有(x-a)2+(y-b)2≥2,”得出关于a,b的点(a,b)的区域,最后再据此不等式组表示的平面区域求出面积即可.
,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,再利用求最优解的方法,结合题中条件:“恒有(x-a)2+(y-b)2≥2,”得出关于a,b的点(a,b)的区域,最后再据此不等式组表示的平面区域求出面积即可. 解:依据不等式组
解:依据不等式组 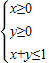 ,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,如图中黄色区域,
,结合二元一次不等式(组)与平面区域的关系画出其表示的平面区域,如图中黄色区域,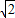 .
.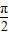 .
.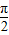 .
.

科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| ab |
查看答案和解析>>
科目:高中数学 来源:月考题 题型:填空题
 时,恒有(x﹣a)2+(y﹣b)2≥2,则以a,b为坐标的点(a,b)所形成的平面区域的面积等于( )
时,恒有(x﹣a)2+(y﹣b)2≥2,则以a,b为坐标的点(a,b)所形成的平面区域的面积等于( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com