错位相减法求和:求和:Sn=1+3x+5x2+7x3+…+(2n-1)xn-1.
【答案】
分析:对x分类讨论,利用“错位相减法”和等差数列的前n项和公式、等比数列的前n项和公式即可得出.
解答:解:由题可知,{(2n-1)x
n-1}的通项是等差数列{2n-1}的通项与等比数列{x
n-1}的通项之积.
∵S
n=1+3x+5x
2+7x
3+…+(2n-1)x
n-1,
∴
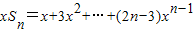
+(2n-1)x
n,
两式相减得(1-x)S
n=1+2x+2x
2+…+2x
n-1-(2n-1)x
n,
①当x≠1,0时,由等比数列的求和公式得:(1-x)S
n=1+
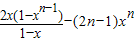
,
∴
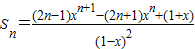
;
②当x=1时,S
n=1+3+5+…+(2n-1)=

=n
2.
③当x=0时,S
n=1+0=1.
点评:熟练掌握分类讨论思想、“错位相减法”、等差数列的前n项和公式、等比数列的前n项和公式是解题的关键.

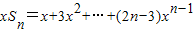 +(2n-1)xn,
+(2n-1)xn,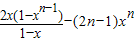 ,
,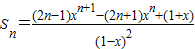 ;
; =n2.
=n2.

 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案